Problem Statement
In this post, I’ll tackle the Facility Location Problem, which involves deciding the optimal placement of facilities to minimize costs. Unlike my previous post on using a genetic algorithm for the TSP, I’ll utilize OR-Tools to solve this problem.
Defining the solver
Referencing the MIP example, I’ll solve the FLP using the MIP approach. Let’s place all solver codes in FLPService.java:
// Create the linear solver with the SCIP backend.
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
System.out.println("Could not create solver SCIP");
return;
}
Defining the variables
Each facility \( j \) in the set of facilities \( J \quad j \in J \)
- A fixed setup cost \( s_j \quad s_j \in \mathbb{R}^+ \)
- A capacity \( c_j \quad c_j \in \mathbb{Z}^+ \)
This is represented in Facility.java:
@Data
@Builder
@AllArgsConstructor
@NoArgsConstructor
@Serdeable.Serializable
public class Facility {
double setupCost;
int capacity;
double x;
double y;
}
Each customer \( i \) in the set of customers \( I \quad i \in I \)
- A demand \( d_i \quad d_i \in \mathbb{Z}^+ \)
This is represented in Customer.java:
@Data
@Builder
@AllArgsConstructor
@NoArgsConstructor
@Serdeable.Serializable
public class Customer {
int demand;
double x;
double y;
}
The delivery cost is proportional to the distance between the facility and the customer, \( dist_{i,j} \quad dist_{i,j} \in \mathbb{R}^+ \).
double[][] dist = new double[customerCount][facilityCount];
Define decision variables:
- \( f_j \) for facility \( j \)
- \( a_{i,j} \) for assigning customer \( i \) to facility \( j \)
// Decision Variables: f[j] is 1 if facility j is opened, otherwise 0
MPVariable[] f = solver.makeIntVarArray(numFacility,0.0, 1.0, "f_");
// Decision Variables: a[i][j] is 1 when customer i is assigned to facility j, otherwise 0
MPVariable[][] a = new MPVariable[numCustomer][numFacility];
for (int i = 0; i < numCustomer; i++) {
a[i] = solver.makeIntVarArray(numFacility, 0.0, 1.0, "a_" + i);
}
Defining the constraints
Each customer must be served by exactly one facility:
$$ \sum_{j \in J} a_{i,j} = 1 \quad \forall i \in I $$// Customer constraint: Each customer is assigned to exactly one facility
for (int i = 0; i < numCustomer; i++) {
MPConstraint constraint = solver.makeConstraint(1.0, 1.0, "customer_" + i);
for (int j = 0; j < numFacility; j++) {
constraint.setCoefficient(a[i][j], 1.0);
}
}
Each facility must meet the demand of its assigned customers without exceeding its capacity:
$$ \sum_{i \in I} (d_i \cdot a_{i,j}) \leq c_j \cdot f_j \quad \forall j \in J $$// Capacity constraint: Facility capacities
for (int j = 0; j < numFacility; j++) {
MPConstraint constraint = solver.makeConstraint(-MPSolver.infinity(), 0.0, "capacity_" + j);
for (int i = 0; i < numCustomer; i++) {
constraint.setCoefficient(a[i][j], customers[i].demand);
}
constraint.setCoefficient(f[j], -facilities[j].capacity);
}
Defining the objective
Minimize the total cost, including setup and delivery costs:
$$ \sum_{j \in J} (f_j \cdot s_j + \sum_{i \in I} a_{i,j} \cdot dist_{i,j}) $$This is implemented as:
// Objective function: minimize total cost (including setup costs and delivery cost)
MPObjective objective = solver.objective();
for (int j = 0; j < numFacility; j++) {
// Add setup cost for each facility
objective.setCoefficient(f[j], facilities[j].setupCost);
for (int i = 0; i < numCustomer; i++) {
// Add delivery cost for assigning each customer to each facility
objective.setCoefficient(a[i][j], dist[i][j]);
}
}
objective.setMinimization();
Displaying the solution
// checks solver output progress
solver.enableOutput();
// sets the max solving time in milliseconds
solver.setTimeLimit(1200000);
// calls the solver
MPSolver.ResultStatus resultStatus = solver.solve();
// Check that the problem has a feasible solution
if (resultStatus == MPSolver.ResultStatus.OPTIMAL || resultStatus == MPSolver.ResultStatus.FEASIBLE) {
System.out.println("Total cost: " + objective.value() + "\n");
for (int j = 0; j < numFacility; ++j) {
double toatlCost = facilities[j].setupCost;
if (f[j].solutionValue() > 0.5) {
double totalDemand = 0;
for (int i = 0; i < numCustomer; ++i) {
if (a[i][j].solutionValue() > 0.0) {
totalDemand += customers[i].demand;
toatlCost += dist[i][j];
}
}
System.out.println("Facility: " + j + ", capacity: " + facilities[j].capacity + ", demand: " + totalDemand + ", cost: " + toatlCost);
}
}
} else {
System.out.println("No solution found.");
}
The input file
Sample input file:
3 8
100 100 1065.0 1065.0
100 100 1062.0 1062.0
100 500 0.0 0.0
50 1397.0 1397.0
50 1398.0 1398.0
75 1399.0 1399.0
75 586.0 586.0
80 900.0 900.0
80 910.0 910.0
90 1200.0 1200.0
90 1210.0 1210.0
Where
- Lines 2- 4 represent facilities (cost, capacity, coordinates)
- Lines 5 -12 represent customers (demand, coordinates)
The solution
The FLPSolution.java:
@Data
@Builder
@AllArgsConstructor
@NoArgsConstructor
@Serdeable.Serializable
public class FLPSolution {
private double objectiveValue;
private Map<String, Double> variableValue;
private String status;
}
Micronaut Service for FLP
The solve method in FLPService.java:
@Singleton
public class FLPService {
FLPSolution solve(Facility[] facilities, Customer[] customers, double[][] dist) {
int numFacility = facilities.length;
int numCustomer = customers.length;
Loader.loadNativeLibraries();
// Create the linear solver with the SCIP backend
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
System.out.println("Could not create solver SCIP");
return;
}
// Define decision variables
MPVariable[] f = solver.makeIntVarArray(numFacility,0.0, 1.0, "f_");
MPVariable[][] a = new MPVariable[numCustomer][numFacility];
for (int i = 0; i < numCustomer; i++) {
a[i] = solver.makeIntVarArray(numFacility, 0.0, 1.0, "a_" + i);
}
// Customer constraint: each customer is assigned to exactly one facility
for (int i = 0; i < numCustomer; i++) {
MPConstraint constraint = solver.makeConstraint(1.0, 1.0, "customer_" + i);
for (int j = 0; j < numFacility; j++) {
constraint.setCoefficient(a[i][j], 1.0);
}
}
// Capacity constraint: facility capacities
for (int j = 0; j < numFacility; j++) {
MPConstraint constraint = solver.makeConstraint(-MPSolver.infinity(), 0.0, "capacity_" + j);
for (int i = 0; i < numCustomer; i++) {
constraint.setCoefficient(a[i][j], customers[i].demand);
}
constraint.setCoefficient(f[j], -facilities[j].capacity);
}
// Objective function: minimize total cost (including setup and delivery cost)
MPObjective objective = solver.objective();
for (int j = 0; j < numFacility; j++) {
objective.setCoefficient(f[j], facilities[j].setupCost);
for (int i = 0; i < numCustomer; i++) {
objective.setCoefficient(a[i][j], dist[i][j]);
}
}
objective.setMinimization();
// Set solver parameters
solver.enableOutput();
solver.setTimeLimit(1200000);
// Solve the problem
MPSolver.ResultStatus resultStatus = solver.solve();
// Prepare the solution
Map<String, Double> variables = new HashMap<>();
if (resultStatus == MPSolver.ResultStatus.OPTIMAL || resultStatus == MPSolver.ResultStatus.FEASIBLE) {
for (int j = 0; j < numFacility; ++j) {
if (f[j].solutionValue() > 0.5) {
for (int i = 0; i < numCustomer; ++i) {
if (a[i][j].solutionValue() > 0.0) {
variables.put("a_" + i + "_" + j, a[i][j].solutionValue());
}
}
variables.put("f_" + j, f[j].solutionValue());
}
}
}
return FLPSolution.builder()
.objectiveValue(objective.value())
.variableValue(variables)
.status(resultStatus.name())
.build();
}
}
This service finds the optimal facility locations, minimizing costs while ensuring each customer’s demand is met.
Micronaut Controller for FLP
The FLPController.java file is responsible for exposing an API endpoint that allows users to upload a file containing the input data for the FLP and then processes that data to find the optimal solution.
Here’s the implementation:
@Controller("/flp")
public class FLPController {
private final FLPService flpService;
public FLPController(FLPService flpService) {
this.flpService = flpService;
}
@Post(value = "/uploadAndSolve", consumes = MediaType.MULTIPART_FORM_DATA)
public FLPSolution uploadAndSolve(CompletedFileUpload file) {
try {
// Read the contents of the file into a List of Strings
List<String> lines = new ArrayList<>();
try (BufferedReader input = new BufferedReader(new InputStreamReader(file.getInputStream(), StandardCharsets.UTF_8))) {
String line;
while ((line = input.readLine()) != null) {
lines.add(line);
}
}
// Process the lines to extract facilities, customers, and distances
Map<String, Object> dataMap = flpService.processLines(lines);
double[][] distances = (double[][]) dataMap.get("distances");
Facility[] facilities = (Facility[]) dataMap.get("facilities");
Customer[] customers = (Customer[]) dataMap.get("customers");
// Solve the FLP with the extracted data
return flpService.solve(facilities, customers, distances);
} catch (IOException e) {
e.printStackTrace();
return null; // or handle error appropriately
}
}
}
The Service Method to Process Input Lines
The processLines method in FLPService parses the input file lines and extracts the necessary data:
@Singleton
public class FLPService {
static {
Loader.loadNativeLibraries();
}
Map<String, Object> processLines(List<String> lines) {
// Extract the number of facilities and customers from the first line
String[] firstLine = lines.get(0).split(" ");
int numFacilities = Integer.parseInt(firstLine[0]);
int numCustomers = Integer.parseInt(firstLine[1]);
// Create arrays for facilities and customers
Facility[] facilities = new Facility[numFacilities];
Customer[] customers = new Customer[numCustomers];
// Parse facility data
for (int i = 1; i < numFacilities + 1; i++) {
String[] facilityData = lines.get(i).split(" ");
facilities[i - 1] = Facility.builder()
.setupCost(Double.parseDouble(facilityData[0])).
capacity(Integer.parseInt(facilityData[1]))
.x(Double.parseDouble(facilityData[2])).
y(Double.parseDouble(facilityData[3])).build();
}
// Parse customer data
for (int i = numFacilities + 1; i < numFacilities + numCustomers + 1; i++) {
String[] customerData = lines.get(i).split(" ");
customers[i - numFacilities - 1] = Customer.builder()
.demand(Integer.parseInt(customerData[0]))
.x(Double.parseDouble(customerData[1]))
.y(Double.parseDouble(customerData[2])).build();
}
// Calculate distances
double[][] distances = new double[numCustomers][numFacilities];
for (int i = 0; i < numCustomers; i++) {
for (int j = 0; j < numFacilities; j++) {
distances[i][j] = calculateDistance(customers[i], facilities[j]);
}
}
// Prepare the result map
Map<String, Object> dataMap = new HashMap<>();
dataMap.put("distances", distances);
dataMap.put("facilities", facilities);
dataMap.put("customers", customers);
return dataMap;
}
private double calculateDistance(Customer customer, Facility facility) {
double dx = customer.getX() - facility.getX();
double dy = customer.getY() - facility.getY();
return Math.sqrt(dx * dx + dy * dy);
}
// The solve method remains the same as defined in the previous sections
}
Summary
This Micronaut setup allows users to upload an input file to solve the Facility Location Problem using the provided FLP service. The controller processes the file, extracts data, and leverages OR-Tools to find the optimal solution.
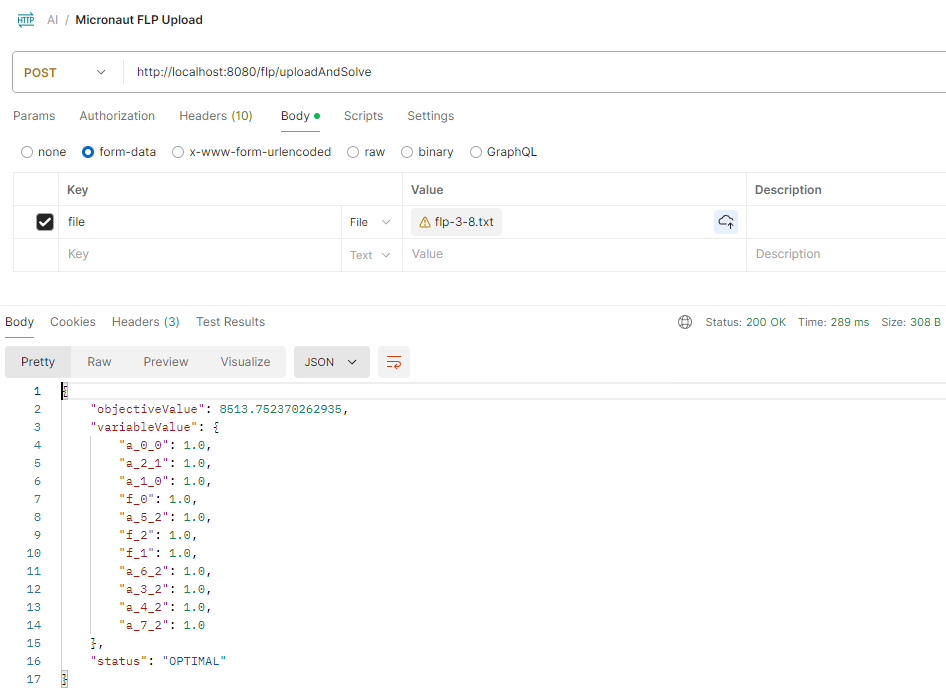
Testing the Controller
To test the controller, you can use tools like Postman to send a POST request with a multipart/form-data containing the input file. The service will process the file and return the solution, which you can inspect in the response.
Sample Solver Output
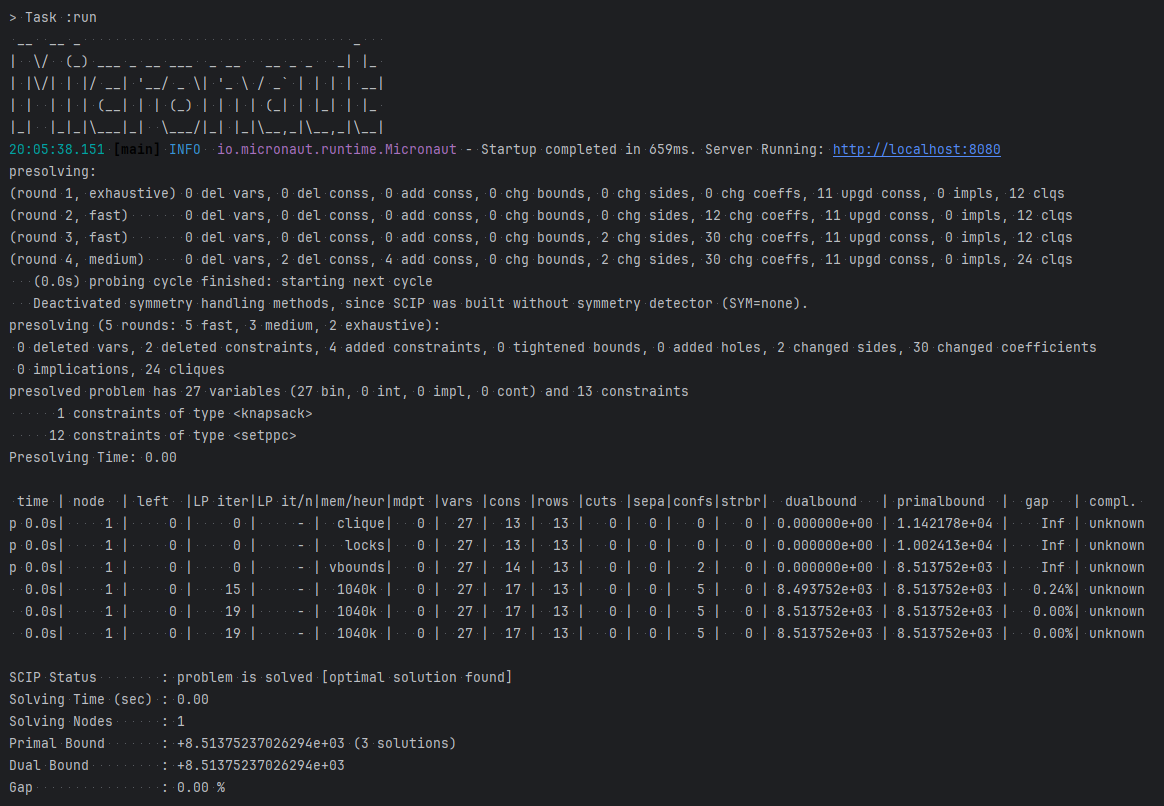
Upon successful upload and processing, you will see the solver’s output with the details of the selected facilities and assigned customers:
And this is the sample solver output from micronaut:
With this setup, you now have a fully functional Micronaut application that can solve the Facility Location Problem based on user-provided input files.