Optimizing TSP with Genetic Algorithms in Micronaut
Problem Statement
Research suggests that the Optimal 85,900-Point Tour is the largest solved instance of the Traveling Salesman Problem (TSP). For this post, I will attempt to solve the TSP problem involving 200 cities.
Genetic algorithms simulate the process of natural selection, mimicking “survival of the fittest” to solve problems. These algorithms evolve over generations, with each generation comprising individuals better adapted to solving the problem.
Referencing Genetic Algorithm for TSP, I documented my solution steps.
Initialisation
I implemented the genome as an int[]. Here’s my Individual.java:
import io.micronaut.serde.annotation.Serdeable;
import lombok.*;
@Data
@Builder
@AllArgsConstructor
@NoArgsConstructor
@Serdeable.Serializable
public class Individual {
int[] genome; // sequence of cities to visit, starting with first city 0
double fitness; // total distance travelled
String message; // additional information attached to the individual
}
Here are the configuration parameters in TspGaService.java:
// Configuration
final int POPULATION_SIZE = 100; // Population size
final int MAX_GENERATIONS = 1200; // Maximum number of generations
final double INITIAL_TEMPERATURE = 1000; // Initial temperature to start with
final double FINAL_TEMPERATURE = 1; // Terminate main loop when temperature reached
final double COOLING_RATE = 0.9995; // Cooling rate
final int FITNESS_MEMO_SIZE = 10000000; // Limit the size of the fitness memo (out of heap size, avoid OOM error)
final int STAGNATION_THRESHOLD = 50; // Number of generations without improvement to trigger action
final int LOCAL_SEARCH_ATTEMPTS = 50; // Number of attempts on local search before exiting local optima
final int MUTATION_ATTEMPTS = 50; // Number of attempts on mutation
int maxCities;
double[][] graph; // Populate with actual distances
double fitnessThreshold; // The desired fitness threshold
int maxStagnationRetry = 10;
ConcurrentHashMap<Integer, Double> fitnessMemo = new ConcurrentHashMap<>(); // Thread-safe memoization for fitness
int generation = 1;
DecimalFormat df = new DecimalFormat("#");
int optimalCount = 0;
In the same class, these helper methods were used:
Individual getIndividual(int[] genome) {
return Individual.builder().genome(genome).fitness(calculateFitness(genome)).build();
}
Individual getIndividual(int[] genome, double fitness) {
return Individual.builder().genome(genome).fitness(fitness).build();
}
// Random number generator function
int randNumber(int start, int end) {
return (int) (Math.random() * (end - start)) + start;
}
double calculateCityDistance(double x1, double y1, double x2, double y2) {
double xDelta = (x1 - x2);
double yDelta = (y1 - y2);
return Math.sqrt((xDelta * xDelta) + (yDelta * yDelta));
}
double calculateDistance(int[] genome) {
double distance = 0;
for (int i = 0; i < genome.length - 1; i++) {
int from = genome[i];
int to = genome[i + 1];
distance += graph[from][to];
}
//NOTE: This is distance needed to travel back to the original city
distance += graph[genome[genome.length-1]][0];
return distance;
}
// Hash-based map for the fitness (total distance of the entire genome)
double calculateFitness(int[] genome) {
int genomeHash = Arrays.hashCode(genome); // Compute the hashcode of entire genome as key, to reduce memory usage
if (fitnessMemo.containsKey(genomeHash)) {
return fitnessMemo.get(genomeHash);
}
double totalDistance = calculateDistance(genome);
if (fitnessMemo.size() < FITNESS_MEMO_SIZE) {
fitnessMemo.put(genomeHash, totalDistance);
}
return totalDistance;
}
// Function to create a genome
int[] createGenome() {
int[] genome = new int[maxCities];
genome[0] = 0;
Set<Integer> newGenome = new HashSet<>();
newGenome.add(0);
int index = 1;
while (newGenome.size() < maxCities) {
int temp = randNumber(1, maxCities);
if (!newGenome.contains(temp)) {
genome[index++] = temp;
newGenome.add(temp);
}
}
return genome;
}
// Convenience method to reinit portion of population
void reinitializePartOfPopulation(List<Individual> population) {
int reinitializeCount = POPULATION_SIZE / 5; // Reinitialize 20% of the population
for (int i = 0; i < reinitializeCount; i++) {
int[] genome = createGenome();
population.set(randNumber(2, population.size()), getIndividual(genome)); // Replace random individuals (excluding the best two)
}
}
List<Individual> initialPopulation() {
List<Individual> population = Collections.synchronizedList(new ArrayList<>());
for (int i = 0; i < POPULATION_SIZE; i++) {
population.add(getIndividual(createGenome()));
}
return population;
}
Local Search
I implemented the 2-opt swap for local search to optimize the tour. My current approach emphasizes breaking the loop as soon as a better solution is found, rather than exhaustively checking all pairs, which would have a complexity of \( O(n^2) \).
double calculateDelta(int[] genome, int i, int j) {
// Calculate the difference in the tour length if the swap (i, j) is made
return graph[genome[i - 1]][genome[j]] + graph[genome[i]][genome[j + 1]]
- graph[genome[i - 1]][genome[i]] - graph[genome[j]][genome[j + 1]];
}
void twoOptSwap(int[] genome, int i, int j) {
while (i < j) {
int temp = genome[i];
genome[i] = genome[j];
genome[j] = temp;
i++;
j--;
}
}
// Few variations, used this as it seems to be work better for both small and large number of cities
int[] localSearch(int[] genome) {
int[] newGenome = genome.clone();
boolean improvement = true;
int iteration = 0;
while (improvement && iteration < LOCAL_SEARCH_ATTEMPTS) {
improvement = false;
for (int i = 1; i < newGenome.length - 2; i++) {
for (int j = i + 1; j < (newGenome.length - 1); j++) {
if (i == j) continue;
double delta = calculateDelta(newGenome, i, j);
if (delta < 0) {
twoOptSwap(newGenome, i, j);
improvement = true;
break; // Early exit on improvement
}
}
if (improvement) break; // Early exit on improvement
}
iteration++;
}
return newGenome;
}
Mutation
To maintain genetic diversity within the population, I implemented three distinct mutation methods:
- Inversion Mutation: Randomly inverts a sequence within the genome.
- Insertion Mutation: Randomly inserts a sequence at a different position within the genome.
- Swap Mutation: Randomly swaps the positions of two genes within the genome.
int[] inversionMutation(int[] genome) {
int[] newGenome = genome.clone();
int start = randNumber(1, maxCities);
int end = randNumber(1, maxCities);
while (start > end) {
end = randNumber(1, maxCities);
}
while (start < end) {
int temp = newGenome[start];
newGenome[start] = newGenome[end];
newGenome[end] = temp;
start++;
end--;
}
return newGenome;
}
int[] insertionMutation(int[] genome) {
int[] newGenome = genome.clone();
int start = randNumber(1, maxCities);
int end = randNumber(1, maxCities);
while (start == end) {
end = randNumber(1, maxCities);
}
int temp = newGenome[start];
if (start < end) {
System.arraycopy(newGenome, start + 1, newGenome, start, end - start);
} else {
System.arraycopy(newGenome, end, newGenome, end + 1, start - end);
}
newGenome[end] = temp;
return newGenome;
}
int[] swapMutation(int[] genome) {
int[] newGenome = genome.clone();
int index1 = randNumber(1, maxCities); // Avoid swapping the first position
int index2 = randNumber(1, maxCities);
int temp = genome[index1];
genome[index1] = genome[index2];
genome[index2] = temp;
return newGenome;
}
// Mutation Operator to maintain diversity in population
int[] mutateGenome(int[] genome) {
int[] newGenome = genome.clone();
int mutationType = randNumber(0, 3); // Adjust to the number of mutation operators
return switch (mutationType) {
case 0 -> inversionMutation(newGenome);
case 1 -> insertionMutation(newGenome);
default -> swapMutation(newGenome);
};
}
int[] performMutation(Individual individual, double temperature) {
int[] newGenome = individual.genome.clone();
double newFitness;
int mutationAttempts = 0;
while (mutationAttempts < MUTATION_ATTEMPTS) {
mutationAttempts++;
newGenome = mutateGenome(newGenome); // Apply mutation
newGenome = localSearch(newGenome); // Integrate local search
newFitness = calculateFitness(newGenome);
if (newFitness < individual.fitness || Math.exp((individual.fitness - newFitness) / temperature) > Math.random()) {
return newGenome;
}
}
// No improvements after mutation attempts
return individual.genome;
}
Crossover
In each generation, the algorithm selects the two fittest individuals to perform crossover. This process creates new offspring by combining genetic material from both parents. A segment of the chromosome is randomly selected from the first parent and incorporated into the offspring. Then, the remaining genes are filled in from the second parent, ensuring that no genes are duplicated. This method blends the characteristics of both parents, producing diverse and potentially more fit offspring for the next generation.
int[] performCrossover(int[] parent1, int[] parent2) {
int length = parent1.length;
int[] child = new int[length];
Set<Integer> usedGenes = new HashSet<>();
// Choose a segment from parent1
int startPos = randNumber(1, length);
int endPos = randNumber(1, length);
// Ensure startPos is less than endPos
if (startPos > endPos) {
int temp = startPos;
startPos = endPos;
endPos = temp;
}
// Copy the segment from parent1 to the child
for (int i = startPos; i < endPos; i++) {
child[i] = parent1[i];
usedGenes.add(parent1[i]);
}
// Ensure the first position is always the starting point
child[0] = 0;
usedGenes.add(0);
// Fill the remaining positions with genes from parent2 in the order they appear
int currentPos = endPos;
for (int i = 1; i < length; i++) {
int geneFromParent2 = parent2[i];
if (!usedGenes.contains(geneFromParent2)) {
usedGenes.add(geneFromParent2);
if (currentPos >= length) {
currentPos = 1; // Wrap around to start filling from the beginning (skipping index 0)
}
if (child[currentPos] == 0) {
child[currentPos] = geneFromParent2;
currentPos++;
}
}
}
// Fill any remaining unfilled positions with random unused genes
for (int i = 1; i < length; i++) {
if (child[i] == 0) {
int rand;
do {
rand = randNumber(1, length);
} while (usedGenes.contains(rand));
child[i] = rand;
usedGenes.add(rand);
}
}
return child;
}
Combining with Simulated Anealling
To enhance the efficiency of solving the problem, I combined the genetic algorithm with simulated annealing. This hybrid approach leverages the strengths of both techniques. The simulated annealing mechanism uses temperature as a probabilistic factor to either accept a better genome or, occasionally, accept a worse genome. This strategy maintains diversity and fosters exploration within the solution space.
The temperature starts high and gradually decreases according to a cooling rate. At higher temperatures, the algorithm is more likely to accept suboptimal solutions, promoting exploration and helping escape local optima. As the temperature drops, the algorithm becomes more selective, favoring better solutions and converging towards an optimal or near-optimal solution.
double adaptiveCooling(double temperature, int generation) {
return temperature * Math.pow(COOLING_RATE, generation / (double) MAX_GENERATIONS);
}
// Combine simulated annealing with genetic algorithm
void simulatedAnnealing(Individual individual, double temperature) {
for (int i = 0; i < 100; i++) { // Simulated annealing iterations
int[] mutatedGenome = mutateGenome(individual.genome);
double mutatedFitness = calculateFitness(mutatedGenome);
if (mutatedFitness < individual.fitness || Math.exp((individual.fitness - mutatedFitness) / temperature) > Math.random()) {
individual.genome = mutatedGenome;
individual.fitness = mutatedFitness;
break;
}
}
}
TspGaService Singleton
This is the TspGaService.java singleton, with the main solve methods:
@Singleton
public class TspGaService {
// Configurations
// Helper methods
// LocalSearch
// Mutation
// Crossover
// Simulated Annealing
Individual solve(double[][] input) {
Instant startTime = Instant.now(); // Record the start time
fitnessMemo.clear();
graph = input;
maxCities = graph.length;
List<Individual> population = initialPopulation();
Individual bestIndividual = null;
double bestFitness = Double.MAX_VALUE;
int stagnationCount = 0;
int stagnationResetCount = 0;
double temperature = INITIAL_TEMPERATURE;
while (temperature > FINAL_TEMPERATURE && generation < MAX_GENERATIONS && stagnationResetCount < maxStagnationRetry) {
// Sort the population by fitness
Collections.sort(population, Comparator.comparingDouble(a -> a.fitness));
// Retain the best two individuals for elitism and crossover
Individual bestCurrentIndividual = population.get(0);
Individual secondBestIndividual = population.get(1);
List<Individual> newPopulation = Collections.synchronizedList(new ArrayList<>());
newPopulation.add(bestCurrentIndividual);
newPopulation.add(secondBestIndividual);
// Perform crossover and mutation
for (int i = 0; i < POPULATION_SIZE; i++) {
int[] newGnome;
if (Math.random() < 0.5) {
newGnome = performCrossover(bestCurrentIndividual.genome, secondBestIndividual.genome);
} else {
Individual randomIndividual = population.get(i);
newGnome = performMutation(randomIndividual, temperature);
}
newGnome = localSearch(newGnome);
Individual newIndividual = getIndividual(newGnome, calculateFitness(newGnome));
simulatedAnnealing(newIndividual, temperature); // Apply simulated annealing
newPopulation.add(newIndividual);
}
// Ensure population is updated correctly
if (!newPopulation.isEmpty()) {
// Use a mix of old and new population to maintain diversity
population = new ArrayList<>(newPopulation);
while (population.size() < POPULATION_SIZE) {
int[] genome = createGenome();
population.add(getIndividual(genome, calculateFitness(genome)));
}
} else {
for (int i = 0; i < POPULATION_SIZE; i++) {
int[] genome = createGenome();
population.add(getIndividual(genome, calculateFitness(genome)));
}
}
// Update temperature regardless of population changes
temperature = adaptiveCooling(temperature, generation);
// Check for stagnation
Individual currentBest = Collections.min(population, Comparator.comparingDouble(a -> a.fitness));
if (currentBest.fitness == bestFitness) {
optimalCount++;
System.out.println("Potentially an optimal solution! " + bestFitness);
if (optimalCount > 3) {
System.out.println("Optimal solution, existing " + bestFitness);
break;
}
} else if (currentBest.fitness < bestFitness) {
optimalCount = 0;
bestIndividual = currentBest;
bestFitness = bestIndividual.fitness;
Duration elapsedDuration = Duration.between(startTime, Instant.now());
System.out.println(elapsedDuration.toSeconds() + ", generation " + generation + ", fitness " + df.format(bestFitness) + ", fitnessMemo " + fitnessMemo.size());
stagnationCount = 0;
} else {
stagnationCount++;
if (stagnationCount >= STAGNATION_THRESHOLD) {
// Increase mutation rate to escape local optima
Duration elapsedDuration = Duration.between(startTime, Instant.now());
System.out.println(elapsedDuration.toSeconds() + ", stagnation detected: " + stagnationResetCount);
reinitializePartOfPopulation(population); // Reinitialize part of the population
stagnationCount = 0; // Reset stagnation count
stagnationResetCount++;
}
}
generation++;
// Check if the current best fitness meets the required threshold
if (bestIndividual != null && bestIndividual.fitness <= fitnessThreshold) {
System.out.println("Reached the fitness threshold. Stopping the algorithm.");
break;
}
}
// Find and print the most efficient path
System.out.println("Most efficient path after " + generation + " generations, threshold=" + fitnessThreshold + ", temp:" +temperature);
return bestIndividual;
}
}
TSPController
Refactored from my previous controller:
@Controller("/tsp")
public class TSPController {
...
private final TspGaService tspGaService;
@Post("/solveGa")
@Produces(MediaType.APPLICATION_JSON)
@Consumes(MediaType.APPLICATION_JSON)
public Individual solveTspGa(@Body double[][] distances) {
return tspGaService.solve(distances);
}
}
Solver in Action
Following these steps, I achieved a solution to the problem, though there is still room for improvement. This approach demonstrates how simulated annealing, genetic algorithms, and local search can collectively address the TSP, even with a large number of cities.
Compared to my previous solver, this algorithm performs significantly better:
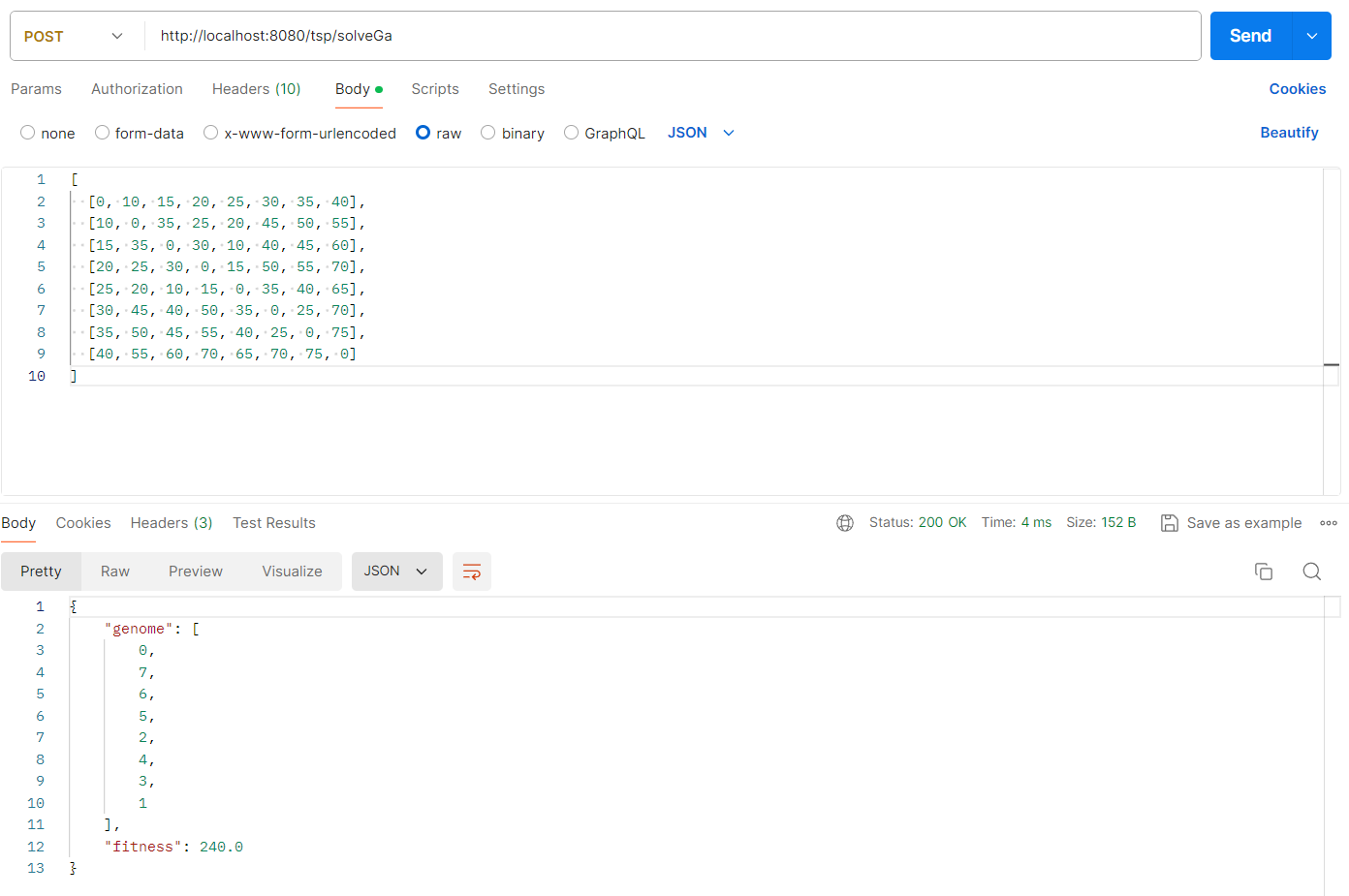
With this custom implementation, here is the result for 51 cities:
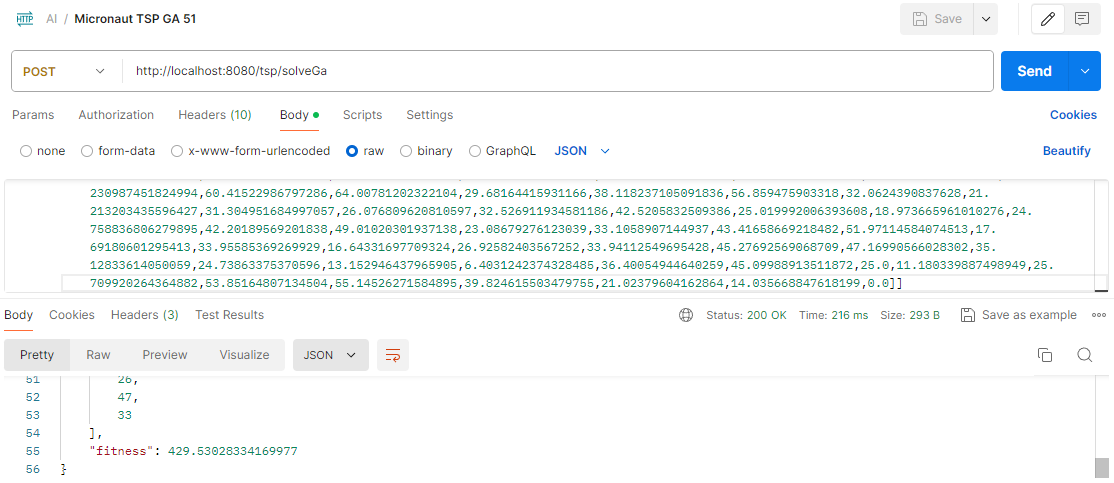
And for 200 cities:
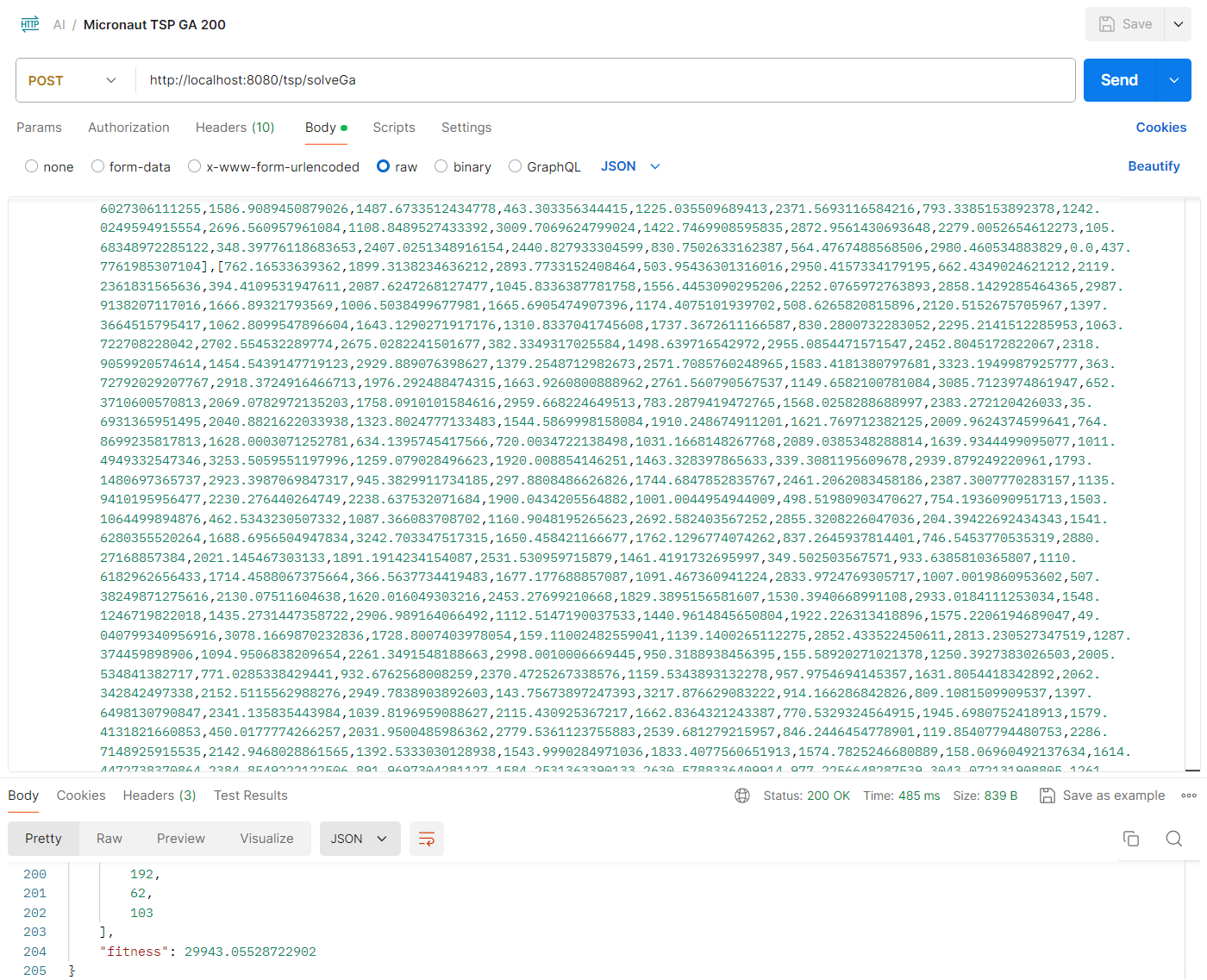
Lesson Learnt
Chat Less, Think More!
While I enjoy discussing algorithms with GPT-4o, sometimes it’s crucial to chat less and think more about the algorithm’s implementation!