GPT-2 Training Guide

October 31, 2024 - 18 mins read

In this post, I’ll build on my previous post, where we set up GPT-2. Following Andrej Karpathy’s instructional video, I’ll walk through each step for training GPT-2 on a small dataset—Tiny Shakespeare. This post is a documentation of my learning journey with GPT-2, closely following Karpathy’s approach.

Training

We’ll use the Tiny Shakespeare dataset to get started:

with open('input.txt', 'r') as f:
    text = f.read()
data = text[:1000]
print(data[:100])

# Sample output:
# First Citizen:
# Before we proceed any further, hear me speak.
# 
# All:
# Speak, speak.
# 
# First Citizen:
# You

To verify the data size, we can use a word count tool in WSL:

wc input.txt
# Output:
# 40000  202651 1115394 input.txt

Encoding the Dataset with tiktoken

Using tiktoken to encode the dataset (GPT-2’s tokenizer), we can observe that 198 represents the newline character:

import tiktoken
enc = tiktoken.get_encoding('gpt2')
tokens = enc.encode(data)
print(tokens[:24])

# [5962, 22307, 25, 198, 8421, 356, 5120, 597, 2252, 11, 3285, 502, 2740, 13, 198, 198, 3237, 25, 198, 5248, 461, 11, 2740, 13]

To break this into sequences, we convert the encoded data into B x T tensors for batching.

import torch
buf = torch.tensor(tokens[:24 + 1])
x = buf[:-1].view(4,6)
y = buf[1:].view(4,6)
print(x) # input tensor
print(y) # label tensor

# tensor([[ 5962, 22307,    25,   198,  8421,   356],
#         [ 5120,   597,  2252,    11,  3285,   502],
#         [ 2740,    13,   198,   198,  3237,    25],
#         [  198,  5248,   461,    11,  2740,    13]])
# tensor([[22307,    25,   198,  8421,   356,  5120],
#         [  597,  2252,    11,  3285,   502,  2740],
#         [   13,   198,   198,  3237,    25,   198],
#         [ 5248,   461,    11,  2740,    13,   198]])

Adding a Loss Function

Let’s define a loss function in the custom GPT model:

class GPT(nn.Module):
    ...
    def forward(self, idx, targets=None):
        # idx is of shape (B, T)
        B, T = idx.size()
        assert T <= self.config.block_size, f"Cannot forward sequence of length {t}, block size is only {self.config.block_size}"
        # forward the token and position embeddings
        pos = torch.arange(0, T, dtype=torch.long, device=idx.device) # shape (t)
        pos_emb = self.transformer.wpe(pos) # position embeddings of shape (t, n_embd)
        tok_emb = self.transformer.wte(idx) # token embeddings of shape (b, t, n_embd)
        x = tok_emb + pos_emb
        # forward the blocks of the transformer
        for block in self.transformer.h:
            x = block(x)
        # forward the final layernorm and the classifier
        x = self.transformer.ln_f(x)        
        logits = self.lm_head(x) # (B, T, vocab_size)
        loss = None
        if targets is not None:
            loss = F.cross_entropy(logits.view(-1, logits.size(-1)), targets.view(-1))
        return logits, loss

device = "cpu"
if torch.cuda.is_available():
    device = "cuda"
elif hasattr(torch.backends, "mps") and torch.backends.mps.is_available():
    device = "mps"
print(f"using device: {device}")

# get a data batch
import tiktoken
enc = tiktoken.get_encoding('gpt2')
with open('input.txt', 'r') as f:
    text = f.read()
text = text[:1000]
tokens = enc.encode(text)
B, T = 4, 32
buf = torch.tensor(tokens[:B*T + 1])
buf = buf.to(device) # move buf to same device
x = buf[:-1].view(B, T)
y = buf[1:].view(B, T)

# get logits
model = GPT(GPTConfig())
model.to(device)
logits, loss = model(x, y)

print(loss)
# using device: cuda
# tensor(11.0591, device='cuda:0', grad_fn=<NllLossBackward0>)

# expected loss at initialization
input = -math.log(1/50257)
print(input)
# 10.82490511970208

Optimizing the Model

We’ll use the AdamW optimizer, which is typically effective for initial GPT training:

# optimize!
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4) # good learning rate for most at the beginning
for i in range(50):
    optimizer.zero_grad() # to always start zero gradient
    logits, loss = model(x, y)
    loss.backward() # deposits or add the gradient 
    optimizer.step() # update parameters, decrease loss
    print(f"step: {i}, loss: {loss.item()}")

# step: 0, loss: 11.059085845947266
# step: 1, loss: 6.672627925872803
# step: 2, loss: 4.326003074645996
# ...
# step: 47, loss: 0.003014578018337488
# step: 48, loss: 0.002937569282948971
# step: 49, loss: 0.002866392722353339

Adding a Simple DataLoader

A lightweight data loader simplifies the batching process by iterating over the encoded data:

import tiktoken

class DataLoaderLite:
    def __init__(self, B, T):
        self.B = B
        self.T = T

        with open('input.txt', 'r') as f:
            text = f.read()
        enc = tiktoken.get_encoding('gpt2')
        tokens = enc.encode(text)
        self.tokens = torch.tensor(tokens)
        print(f"loaded {len(self.tokens)} tokens")
        print(f"1 epoch = {len(self.tokens) // (B * T)} batches")

        self.current_position = 0

    def next_batch(self):
        B, T = self.B, self.T
        buf = self.tokens[self.current_position : self.current_position+B*T+1]
        x = buf[:-1].view(B, T) # inputs
        y = buf[1:].view(B, T) # targets
        # advance the position in the tensor
        self.current_position += B * T
        # if loading the next batch would be out of bounds, reset
        if self.current_position + (B * T +1) > len(self.tokens):
            self.current_position = 0
        return x, y

train_loader = DataLoaderLite(B=4, T=32)

# get logits
model = GPT(GPTConfig())
model.to(device)

# optimize!
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4)
for i in range(50):
    x, y = train_loader.next_batch()
    x, y = x.to(device), y.to(device) # move tensor to device
    optimizer.zero_grad()
    logits, loss = model(x, y)
    loss.backward()
    optimizer.step()
    print(f"step: {i}, loss: {loss.item()}")

# loaded 338025 tokens
# 1 epoch = 2640 batches
# step: 0, loss: 11.003260612487793
# step: 1, loss: 9.66711139678955
# step: 2, loss: 8.685151100158691    
# ...
# step: 47, loss: 5.960447311401367
# step: 48, loss: 6.783339500427246
# step: 49, loss: 6.529984474182129

Using Pretrained GPT-2 Parameters

Leveraging pretrained weights can enhance performance. Here, we validate that GPT-2’s top and bottom layers share weights:

from transformers import GPT2LMHeadModel
model_hf = GPT2LMHeadModel.from_pretrained("gpt2") #124M
sd_hf = model_hf.state_dict()

print(sd_hf["lm_head.weight"].shape)
print(sd_hf["transformer.wte.weight"].shape)
result = (sd_hf["lm_head.weight"] == sd_hf["transformer.wte.weight"]).all()
print(result)
print(sd_hf["transformer.wte.weight"].data_ptr)
print(sd_hf["transformer.wte.weight"].data_ptr)

# torch.Size([50257, 768])
# torch.Size([50257, 768])
# tensor(True)
# <built-in method data_ptr of Tensor object at 0x00000254ECD982D0>
# <built-in method data_ptr of Tensor object at 0x00000254ECD982D0>

Implementing Weight Sharing in Our Model

To enable weight sharing, we set the embedding and head layers to use the same weights:

class GPT(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.transformer = nn.ModuleDict(dict(
            wte = nn.Embedding(config.vocab_size, config.n_embd),
            wpe = nn.Embedding(config.block_size, config.n_embd),
            h = nn.ModuleList([Block(config) for _ in range(config.n_layer)]),
            ln_f = nn.LayerNorm(config.n_embd),
        ))
        self.lm_head = nn.Linear(config.n_embd, config.vocab_size, bias=False)
        # weight sharing scheme
        self.transformer.wte.weight = self.lm_head.weight
        ...

Initializing Parameters

Proper initialization of parameters, such as in self-attention blocks, is crucial to stable training.

class CausalSelfAttention(nn.Module):
    def __init__(self, config):
        super().__init__()
        assert config.n_embd % config.n_head == 0
        # key, query, value projections for all heads, but in a batch
        self.c_attn = nn.Linear(config.n_embd, 3 * config.n_embd)
        # output projection
        self.c_proj = nn.Linear(config.n_embd, config.n_embd)
        self.c_proj.NANOGPT_SCALE_INIT = 1
        # regularization
        self.n_head = config.n_head
        self.n_embd = config.n_embd
        self.register_buffer("bias", torch.tril(torch.ones(config.block_size, config.block_size))
                                    .view(1, 1, config.block_size, config.block_size))

    def forward(self, x):
        B, T, C = x.size() # batch size, sequence length, embedding dimensionality (n_embd)
        qkv  = self.c_attn(x)
        q, k, v = qkv.split(self.n_embd, dim=2)
        k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        # attention (materializes the large (T,T) matrix for all the queries and keys)

        att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
        att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
        att = F.softmax(att, dim=-1)
        y = att @ v # (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
        
        y = y.transpose(1, 2).contiguous().view(B, T, C) # re-assemble all head outputs side by side
        # output projection
        y = self.c_proj(y)
        return y

class MLP(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.c_fc    = nn.Linear(config.n_embd, 4 * config.n_embd)
        self.gelu    = nn.GELU(approximate='tanh')
        self.c_proj  = nn.Linear(4 * config.n_embd, config.n_embd)
        self.c_proj.NANOGPT_SCALE_INIT = 1
        
    def forward(self, x):
        x = self.c_fc(x)
        x = self.gelu(x)
        x = self.c_proj(x)
        return x

class GPT(nn.Module):
    def __init__(self, config):
    ...
        # init all weights
        self.apply(self._init_weights)

    def _init_weights(self, module):
        if isinstance(module, nn.Linear):
            std = 0.02
            if hasattr(module, 'NANOGPT_SCALE_INIT'):
                std *= (2 * self.config.n_layer) ** -0.5
            torch.nn.init.normal_(module.weight, mean=0.0, std=std)
            if module.bias is not None:
                torch.nn.init.zeros_(module.bias)
        elif isinstance(module, nn.Embedding):
            torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)
    ...

torch.manual_seed(1337)
if torch.cuda.is_available():
    torch.cuda.manual_seed(1337)

train_loader = DataLoaderLite(B=4, T=32)

# get logits
model = GPT(GPTConfig())
model.to(device)

# optimize!
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4)
for i in range(50):
    x, y = train_loader.next_batch()
    x, y = x.to(device), y.to(device) # move tensor to device
    optimizer.zero_grad()
    logits, loss = model(x, y)
    loss.backward()
    optimizer.step()
    print(f"step: {i}, loss: {loss.item()}")

# loaded 338025 tokens
# 1 epoch = 2640 batches
# step: 0, loss: 10.960028648376465
# step: 1, loss: 9.68770694732666
# step: 2, loss: 9.082900047302246
# ...
# step: 48, loss: 6.953257083892822
# step: 49, loss: 6.799217224121094

Training Performance Insights

Understanding the Hardware

The Jetson Orin NX 16GB boasts 100 TOPS (INT8) and 32 tensor cores, making it ideal for inferencing over training. Thus, for training, I will leverage my 6GB RTX A2000, which delivers a single-precision performance of 8 TFLOPS and 104 tensor cores.

Data type inspection: Using torch.float32 by default

import code; code.interact(local=locals())
# enter below in the interactive prompt for inspection
logits.dtype

To clear cache:

# empty cache
import gc
gc.collect()
torch.cuda.empty_cache()

To watch NVIDIA memory usage in WSL:

watch -n 0.1 nvidia-smi

Booast Training Performance

Automatic Mixed Precision Training: Leverage torch.autocast for efficient mixed precision training

import time

train_loader = DataLoaderLite(B=16, T=1024)
torch.set_float32_matmul_precision('high')

# get logits
model = GPT(GPTConfig())
model.to(device)

# optimize!
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4)
for i in range(50):
    t0 = time.time()
    x, y = train_loader.next_batch()
    x, y = x.to(device), y.to(device)
    optimizer.zero_grad()
    with torch.autocast(device_type=device, dtype=torch.bfloat16):
        logits, loss = model(x, y)     
    loss.backward()
    optimizer.step()
    torch.cuda.synchronize() # wait for GPU to finish work
    t1 = time.time()
    dt = (t1 - t0)*1000
    tokens_per_sec = (train_loader.B * train_loader.T) / (t1 - t0)
    print(f"step: {i} | loss: {loss.item()} | norm: {norm:.4f} | dt: {dt:.2f}ms, tok/sec: {tokens_per_sec:.2f}")

Compile Optimization: Use torch.compile to accelerate code execution

# get logits
model = GPT(GPTConfig())
model.to(device)

import torch._dynamo
torch._dynamo.config.suppress_errors = True
model = torch.compile(model)

Flash Attention: Integrate flash attention to enhance your model’s attention mechanism

class CausalSelfAttention(nn.Module):
    ...
    def forward(self, x):
        B, T, C = x.size() # batch size, sequence length, embedding dimensionality (n_embd)
        qkv  = self.c_attn(x)
        q, k, v = qkv.split(self.n_embd, dim=2)
        k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        # attention (materializes the large (T,T) matrix for all the queries and keys)

        # att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
        # att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
        # att = F.softmax(att, dim=-1)
        # y = att @ v # (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
        y = F.scaled_dot_product_attention(q, k, v, is_causal=True)
        
        y = y.transpose(1, 2).contiguous().view(B, T, C) # re-assemble all head outputs side by side
        # output projection
        y = self.c_proj(y)
        return y

Utilize Efficient Numbers: Optimize computations by using nice numbers

# get logits
model = GPT(GPTConfig(vocab_size=50304))
model.to(device)

# loaded 338025 tokens
# 1 epoch = 20 batches
# step: 0 | loss: 11.026554107666016 | norm: 27.6531 | dt: 4550.37ms, tok/sec: 3600.59
# step: 1 | loss: 9.354239463806152 | norm: 6.2953 | dt: 7496.54ms, tok/sec: 2185.54
# step: 2 | loss: 8.961758613586426 | norm: 2.2035 | dt: 7598.34ms, tok/sec: 2156.26

Gradient Clipping: Clip the global norm of gradients to 1.0 to stabilize training

# optimize!
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4, betas=(0.9, 0.95), eps=1e-8)
for i in range(50):
    t0 = time.time()
    x, y = train_loader.next_batch()
    x, y = x.to(device), y.to(device)
    optimizer.zero_grad()
    with torch.autocast(device_type=device, dtype=torch.bfloat16):
        logits, loss = model(x, y)
    loss.backward()
    norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
    optimizer.step()
    torch.cuda.synchronize() # wait for GPU to finish work
    t1 = time.time()
    dt = t1 - t0 # time difference in seconds
    tokens_per_sec = (train_loader.B * train_loader.T) / (t1 - t0)
    print(f"step: {i} | loss: {loss.item()} | norm: {norm:.4f} | dt: {dt*1000:.2f}ms, tok/sec: {tokens_per_sec:.2f}")

# step: 0 | loss: 6.1148786544799805 | norm: 5.3749 | dt: 5243.35ms, tok/sec: 3124.72
# step: 1 | loss: 5.990167617797852 | norm: 2.5040 | dt: 5465.20ms, tok/sec: 2997.88
# step: 2 | loss: 6.073593616485596 | norm: 1.6870 | dt: 7355.99ms, tok/sec: 2227.30

Learning Rate Setting: Adjust and set an appropriate learning rate for your model

max_lr = 6e-4
min_lr = max_lr * 0.1
warmup_steps = 10
max_steps = 50
def get_lr(it):
    # linear warmup for warmup_iters steps
    if it < warmup_steps:
        return max_lr * (it+1) / warmup_steps
    # if it > lr_decay_iters, return min learning rate
    if it > max_steps:
        return min_lr
    # in between, use cosine decay down to min learning rate
    decay_ratio = (it - warmup_steps) / (max_steps - warmup_steps)
    assert 0 <= decay_ratio <= 1
    coeff = 0.5 * (1.0 + math.cos(math.pi * decay_ratio)) # coeff starts at 1 and goes to 0
    return min_lr + coeff * (max_lr - min_lr)

# optimize!
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4, betas=(0.9, 0.95), eps=1e-8)
for step in range(max_steps):
    t0 = time.time()
    x, y = train_loader.next_batch()
    x, y = x.to(device), y.to(device)
    optimizer.zero_grad()
    with torch.autocast(device_type=device, dtype=torch.bfloat16):
        logits, loss = model(x, y)
    loss.backward()
    norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
    # determine and set the learning rate for this iteration
    lr = get_lr(step)
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr
    optimizer.step()
    torch.cuda.synchronize() # wait for GPU to finish work
    t1 = time.time()
    dt = t1 - t0 # time difference in seconds
    tokens_per_sec = (train_loader.B * train_loader.T) / (t1 - t0)
    print(f"step: {step:4d} | loss: {loss.item()} | norm: {norm:.4f} | dt: {dt*1000:.2f}ms, tok/sec: {tokens_per_sec:.2f}")
# step:    0 | loss: 10.976452 | lr: 0.0001 | norm: 29.3385 | dt: 5638.74ms, tok/sec: 2905.61
# step:    1 | loss: 9.567224 | lr: 0.0001 | norm: 11.2004 | dt: 7997.90ms, tok/sec: 2048.54
# step:    2 | loss: 9.393660 | lr: 0.0002 | norm: 11.4306 | dt: 7960.79ms, tok/sec: 2058.09

Weight Decay: Apply weight decay to regularize your model and prevent overfitting

class GPT(nn.Module):
    ...
    def configure_optimizers(self, weight_decay, learning_rate, device):
        # start with all of the candidate parameters (that require grad)
        param_dict = {pn: p for pn, p in self.named_parameters()}
        param_dict = {pn: p for pn, p in param_dict.items() if p.requires_grad}
        # create optim groups. Any parameters that is 2D will be weight decayed, otherwise no.
        # i.e. all weight tensors in matmuls + embeddings decay, all biases and layernorms don't.
        decay_params = [p for n, p in param_dict.items() if p.dim() >= 2]
        nodecay_params = [p for n, p in param_dict.items() if p.dim() < 2]
        optim_groups = [
            {'params': decay_params, 'weight_decay': weight_decay},
            {'params': nodecay_params, 'weight_decay': 0.0}
        ]
        num_decay_params = sum(p.numel() for p in decay_params)
        num_nodecay_params = sum(p.numel() for p in nodecay_params)
        print(f"num decayed parameter tensors: {len(decay_params)}, with {num_decay_params:,} parameters")
        print(f"num non-decayed parameter tensors: {len(nodecay_params)}, with {num_nodecay_params:,} parameters")
        # Create AdamW optimizer and use the fused version if it is available
        fused_available = 'fused' in inspect.signature(torch.optim.AdamW).parameters
        use_fused = fused_available and 'cuda' in device
        print(f"using fused AdamW: {use_fused}")
        optimizer = torch.optim.AdamW(optim_groups, lr=learning_rate, betas=(0.9, 0.95), eps=1e-8)
        return optimizer

# optimize!
optimizer = model.configure_optimizers(weight_decay=0.1, learning_rate=6e-4, device=device)
...

# num decayed parameter tensors: 50, with 124,354,560 parameters
# num non-decayed parameter tensors: 98, with 121,344 parameters
# using fused AdamW: True

Simulated Batch Accumulation: Effectively using smaller batch sizes when memory is limited by accumulating gradients

for step in range(max_steps):
    t0 = time.time()
    optimizer.zero_grad()
    loss_accum = 0.0
    for micro_step in range(grad_accum_steps):
        x, y = train_loader.next_batch()
        x, y = x.to(device), y.to(device)
        with torch.autocast(device_type=device, dtype=torch.bfloat16):
            logits, loss = model(x, y)
        # we have to scale the loss to account for gradient accumulation,
        # because the gradients just add on each successive backward(),
        # addition of gradients corresponds to a SUM in the objective, but
        # instead of a SUM we want MEAN. Scale the loss here so it comes out right
        loss = loss / grad_accum_steps
        loss_accum += loss.detach()
        loss.backward()
    norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
    # determine and set the learning rate for this iteration
    lr = get_lr(step)
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr
    optimizer.step()
    torch.cuda.synchronize() # wait for GPU to finish work
    t1 = time.time()
    dt = t1 - t0 # time difference in seconds
    tokens_processed = train_loader.B * train_loader.T * grad_accum_steps
    tokens_per_sec = tokens_processed / dt
    print(f"step: {step:4d} | loss: {loss_accum.item():.6f} | lr: {lr:.4f} | norm: {norm:.4f} | dt: {dt*1000:.2f}ms, tok/sec: {tokens_per_sec:.2f}")

# Output for micro batch size, B = 4
# using device: cuda
# total desired batch size: 524288
# => calculated gradient accumulation steps: 128
# loaded 338025 tokens
# 1 epoch = 82 batches
# num decayed parameter tensors: 50, with 124,354,560 parameters
# num non-decayed parameter tensors: 98, with 121,344 parameters
# using fused AdamW: True
# step:    0 | loss: 10.939045 | lr: 0.0001 | norm: 27.0274 | dt: 40582.00ms | tok/sec: 12919.22
# step:    1 | loss: 9.647425 | lr: 0.0001 | norm: 9.5036 | dt: 37164.44ms | tok/sec: 14107.25
# step:    2 | loss: 9.226212 | lr: 0.0002 | norm: 5.7323 | dt: 37072.59ms | tok/sec: 14142.20
# ...
# step:   48 | loss: 5.837780 | lr: 0.0001 | norm: 0.1336 | dt: 36719.26ms | tok/sec: 14278.28
# step:   49 | loss: 5.839324 | lr: 0.0001 | norm: 0.1318 | dt: 36749.97ms | tok/sec: 14266.35

The code at this stage is extracted from train_gpt2.py.

nanoGPT

nanoGPT is an efficient, streamlined repository for training and fine-tuning medium-sized GPT models.

# Clone the repository
git clone https://github.com/karpathy/nanoGPT.git

# Install required packages
pip install torch numpy transformers datasets tiktoken wandb tqdm

# Prepare the dataset
python data/shakespeare_char/prepare.py
# Output:
# length of dataset in characters: 1,115,394
# all the unique characters:
#  !$&',-.3:;?ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
# vocab size: 65
# train has 1,003,854 tokens
# val has 111,540 tokens

Training a Baby GPT Model

The training process for the baby GPT model on my setup:

python train.py config/train_shakespeare_char.py

## Sample Output:
# iter 0: loss 4.2659, time 16.77s, mfu -100.00%
# iter 10: loss 3.2412, time 0.75s, mfu 0.02%
# iter 20: loss 2.7942, time 0.99s, mfu 0.07%
# ...
# step 1750: train loss 1.1015, val loss 1.4632
# saving checkpoint to out-shakespeare-char
# iter 1750: loss 1.1848, time 14.39s, mfu 0.36%
# ...
# iter 4990: loss 0.8243, time 1.03s, mfu 0.36%
# step 5000: train loss 0.6277, val loss 1.6922
# iter 5000: loss 0.8236, time 14.28s, mfu 0.36%

train-llm2-baby-gpt-model

Below are the modifications I applied to the repository:

diff --git a/train.py b/train.py
index 951bda9..b4b386c 100644
--- a/train.py
+++ b/train.py
@@ -205,6 +205,8 @@ checkpoint = None # free up memory
 if compile:
     print("compiling the model... (takes a ~minute)")
     unoptimized_model = model
+    import torch._dynamo
+    torch._dynamo.config.suppress_errors = True
     model = torch.compile(model) # requires PyTorch 2.0

 # wrap model into DDP container
@@ -315,8 +317,6 @@ while True:

     # timing and logging
     t1 = time.time()
-    dt = t1 - t0
-    t0 = t1
     if iter_num % log_interval == 0 and master_process:
         # get loss as float. note: this is a CPU-GPU sync point
         # scale up to undo the division above, approximating the true total loss (exact would have been a sum)
@@ -324,7 +324,9 @@ while True:
         if local_iter_num >= 5: # let the training loop settle a bit
             mfu = raw_model.estimate_mfu(batch_size * gradient_accumulation_steps, dt)
             running_mfu = mfu if running_mfu == -1.0 else 0.9*running_mfu + 0.1*mfu
-        print(f"iter {iter_num}: loss {lossf:.4f}, time {dt*1000:.2f}ms, mfu {running_mfu*100:.2f}%")
+        dt = t1 - t0
+        t0 = t1
+        print(f"iter {iter_num}: loss {lossf:.4f}, time {dt:.2f}s, mfu {running_mfu*100:.2f}%")
     iter_num += 1
     local_iter_num += 1

Sampling with Baby GPT

I ran a sampling script to test the model:

python sample.py --out_dir=out-shakespeare-char

train-llm2-sample-baby-gpt-model

Optional - Integrating with MLflow

For a detailed overview of setting up MLflow alongside Kubeflow, refer to my MLflow integration post. Here’s an example of how I publish training metrics to MLflow:

# optimize!
optimizer = model.configure_optimizers(weight_decay=0.1, learning_rate=6e-4, device=device)

import mlflow
import os 
os.environ['MLFLOW_TRACKING_USERNAME'] = 'user' 
os.environ['MLFLOW_TRACKING_PASSWORD'] = '39VpDZdVLr'

mlflow.set_tracking_uri(uri="http://192.168.68.220")
mlflow.set_experiment("nanoGPT-shakespeare")

mlflow.log_param("Micro Batch Size", B)
mlflow.log_param("Block Size", T)
mlflow.log_param("Batch Size", total_batch_size)
mlflow.log_param("Gradient Accumulation Steps", grad_accum_steps)

for step in range(max_steps):
    t0 = time.time()
    optimizer.zero_grad()
    loss_accum = 0.0
    for micro_step in range(grad_accum_steps):
        x, y = train_loader.next_batch()
        x, y = x.to(device), y.to(device)
        scaler = torch.amp.GradScaler('cuda')
        with torch.autocast(device_type=device, dtype=torch.bfloat16):
            logits, loss = model(x, y)
        # we have to scale the loss to account for gradient accumulation,
        # because the gradients just add on each successive backward(),
        # addition of gradients corresponds to a SUM in the objective, but
        # instead of a SUM we want MEAN. Scale the loss here so it comes out right
        loss = loss / grad_accum_steps
        loss_accum += loss.detach()
        loss.backward()

    norm = torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
    # determine and set the learning rate for this iteration
    lr = get_lr(step)
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr
    optimizer.step()
    torch.cuda.synchronize() # wait for GPU to finish work
    t1 = time.time()
    dt = t1 - t0 # time difference in seconds
    tokens_processed = train_loader.B * train_loader.T * grad_accum_steps
    tokens_per_sec = tokens_processed / dt

    mlflow.log_metric("Loss", loss_accum.item())
    mlflow.log_metric("Learning Rate", lr)
    mlflow.log_metric("Norm", norm)
    mlflow.log_metric("Time per Iteration", dt)
    mlflow.log_metric("Tokens per Second", tokens_per_sec)
    print(f"step: {step:4d} | loss: {loss_accum.item():.6f} | lr: {lr:.4f} | norm: {norm:.4f} | dt: {dt*1000:.2f}ms | tok/sec: {tokens_per_sec:.2f}")

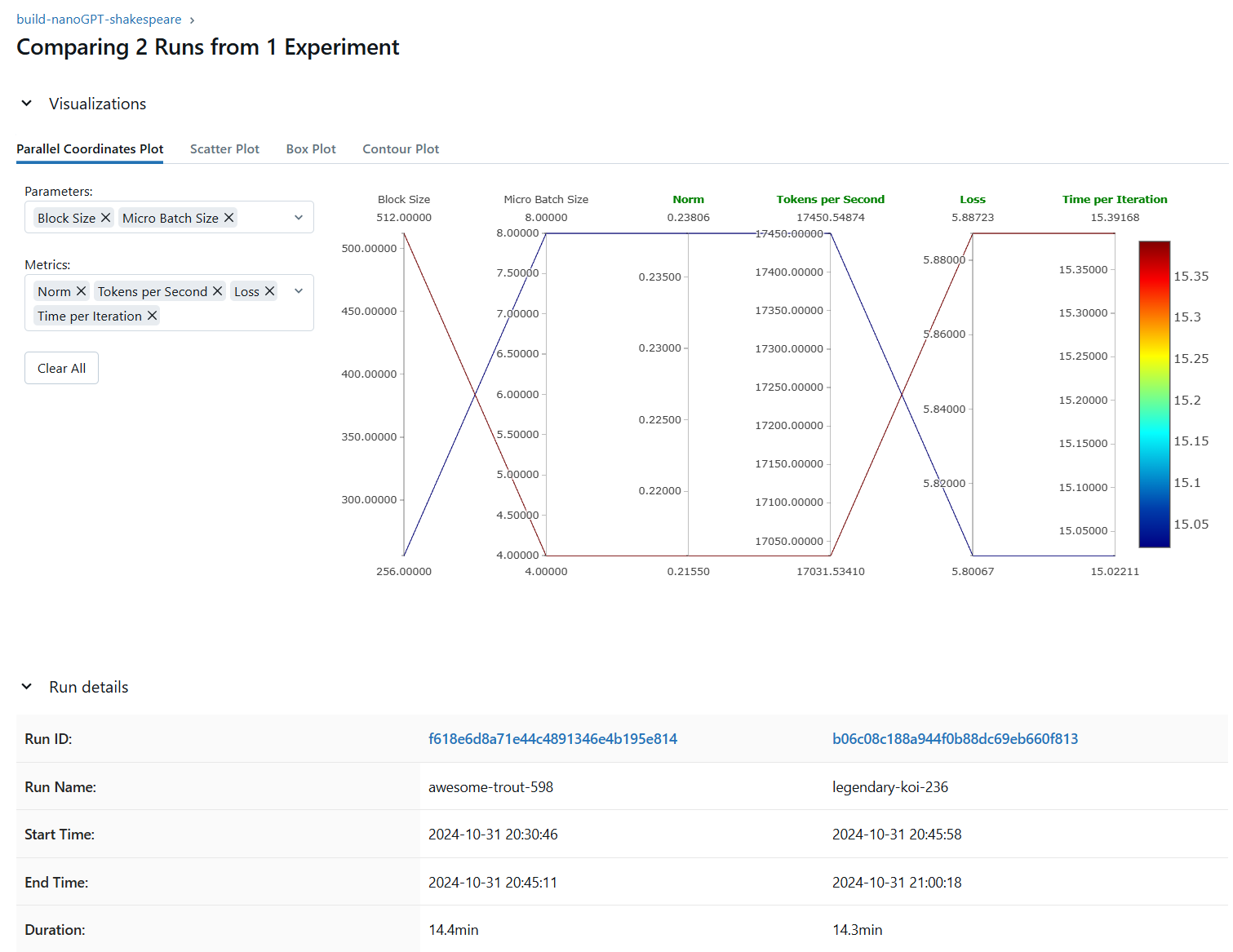
For comparison purpose, these are my settings for the 2 runs:

# 1st run
total_batch_size = 262144
B = 4
T = 512
warmup_steps = 15
# GPU usage around 4821MiB / 6138MiB
# step:    0 | loss: 10.940472 | lr: 0.0001 | norm: 26.5947 | dt: 23285.35ms | tok/sec: 11257.89
# step:    1 | loss: 9.651522 | lr: 0.0001 | norm: 9.2193 | dt: 14724.37ms | tok/sec: 17803.41
# step:    2 | loss: 9.175361 | lr: 0.0002 | norm: 4.7185 | dt: 14595.11ms | tok/sec: 17961.08
# ...
# step:   48 | loss: 5.898010 | lr: 0.0001 | norm: 0.2110 | dt: 15174.01ms | tok/sec: 17275.85
# step:   49 | loss: 5.887230 | lr: 0.0001 | norm: 0.2155 | dt: 15391.68ms | tok/sec: 17031.53

# 2nd run
total_batch_size = 262144
B = 8
T = 256
warmup_steps = 20
# GPU usage around 4821MiB / 6138MiB
# step:    0 | loss: 10.936398 | lr: 0.0001 | norm: 26.1147 | dt: 22972.23ms | tok/sec: 11411.34
# step:    1 | loss: 9.640186 | lr: 0.0001 | norm: 8.7945 | dt: 14762.45ms | tok/sec: 17757.48
# step:    2 | loss: 9.145591 | lr: 0.0002 | norm: 3.6486 | dt: 14683.03ms | tok/sec: 17853.53
...
# step:   48 | loss: 5.813196 | lr: 0.0001 | norm: 0.3081 | dt: 15273.17ms | tok/sec: 17163.70
# step:   49 | loss: 5.800667 | lr: 0.0001 | norm: 0.2381 | dt: 15022.11ms | tok/sec: 17450.55

train-llm2-mlflow-compare-runs