GPT-2 Setup and Pretraining Guide
In this post, I’ll document my journey in learning how to reproduce GPT-2 from scratch using my 6GB NVIDIA RTX A2000 GPU. This is my first attempt at training a model from scratch, and I’m excited to learn from the experts and share my experiences here.
The Basics
I began my journey with the video Create a Large Language Model from Scratch with Python by Elliot Arledge. This video covers the fundamentals of large language models (LLMs) and demonstrates how to build one from the ground up. Here, I’ve documented the foundational concepts I extracted from the initial stages of this video.
PyTorch Basic Examples
As part of this journey, I’m learning PyTorch, an optimized tensor library for deep learning on GPUs and CPUs. In PyTorch, tensors are specialized data structures similar to arrays and matrices, with additional capabilities that make them suitable for deep learning.
import torch
device = (
"cuda"
if torch.cuda.is_available()
else "mps"
if torch.backends.mps.is_available()
else "cpu"
)
print(f"Using {device} device")
# Output: Using cuda device
The shape of a tensor in PyTorch refers to its dimensions — the number of elements along each axis. For example, a tensor with shape (2, 3, 4) means:
- 2 elements along the first axis (depth)
- 3 elements along the second axis (height)
- 4 elements along the third axis (width)
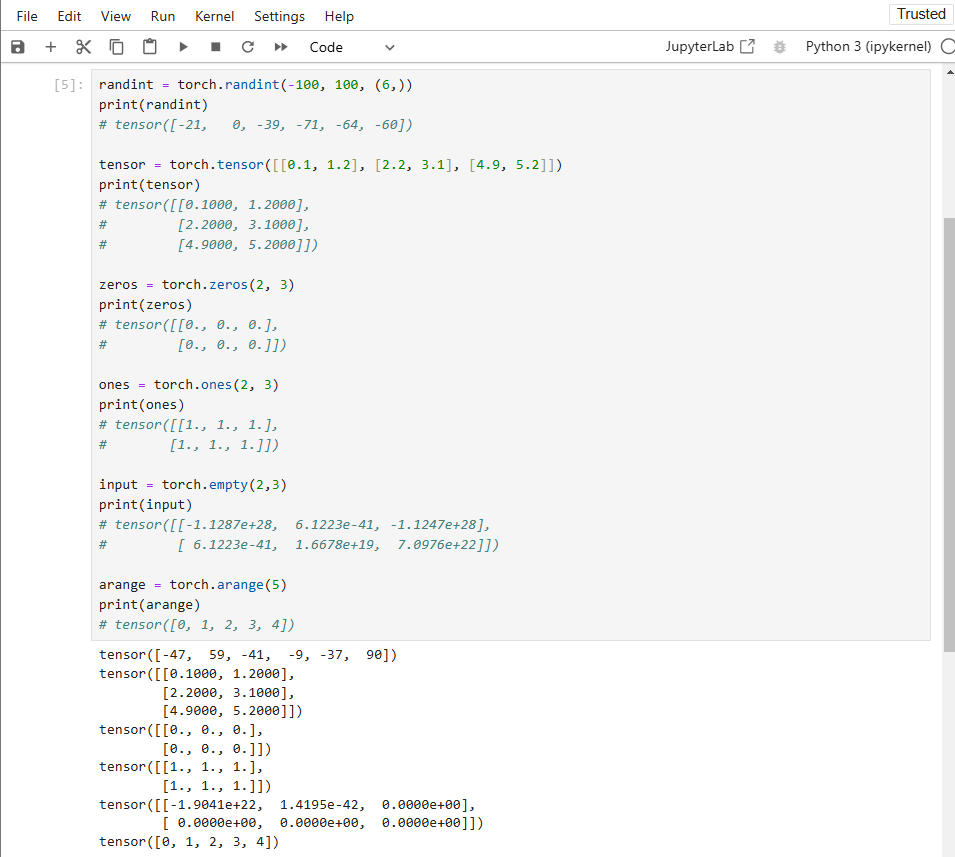
Here are some of the torch functions:
randint = torch.randint(-100, 100, (6,))
print(randint)
# Output: tensor([-21, 0, -39, -71, -64, -60])
tensor = torch.tensor([[0.1, 1.2], [2.2, 3.1], [4.9, 5.2]])
print(tensor)
# tensor([[0.1000, 1.2000],
# [2.2000, 3.1000],
# [4.9000, 5.2000]])
zeros = torch.zeros(2, 3)
print(zeros)
# tensor([[0., 0., 0.],
# [0., 0., 0.]])
ones = torch.ones(2, 3)
print(ones)
# tensor([[1., 1., 1.],
# [1., 1., 1.]])
input = torch.empty(2,3)
print(input)
# tensor([[-1.1287e+28, 6.1223e-41, -1.1247e+28],
# [ 6.1223e-41, 1.6678e+19, 7.0976e+22]])
arange = torch.arange(5)
print(arange)
# tensor([0, 1, 2, 3, 4])
Measuring Time Taken
By using the %%time magic command at the beginning of a cell, I can measure how long the entire cell takes to run, which helps track and optimize execution time.
%%time
import time
start_time = time.time()
zeros = torch.zeros(1, 1)
end_time = time.time()
elapsed_time = end_time - start_time
print(f"{elapsed_time:.8f}")
# Output: 0.00000000 seconds
# CPU times: total: 0 ns
# Wall time: 0 ns
Additional PyTorch Features
Here are some additional PyTorch functions I explored, which I’ll use later in the model-building process. I also explored tril, triu, and masked_fill for manipulating tensor data, and transpose for altering tensor dimensions. These will be helpful for matrix operations and attention mechanisms.
# Returns a tensor where each row contains num_samples indices sampled from the multinomial distribution located in the corresponding row of tensor input
input = torch.tensor([0.1, 0.9])
samples = torch.multinomial(input, num_samples=10, replacement=True)
print(samples)
# Output: tensor([1, 1, 1, 0, 1, 1, 0, 1, 1, 1])
# Concatenates the given sequence of tensors in tensors in the given dimension
tensor = torch.tensor([1, 2, 3, 4])
out = torch.cat((tensor, torch.tensor([5])), dim=0)
print(out)
# tensor([1, 2, 3, 4, 5])
# Returns the lower triangular part of the matrix (2-D tensor), the other elements of the result tensor out are set to 0
out = torch.tril(torch.ones(5, 5))
print(out)
# tensor([[1., 0., 0., 0., 0.],
# [1., 1., 0., 0., 0.],
# [1., 1., 1., 0., 0.],
# [1., 1., 1., 1., 0.],
# [1., 1., 1., 1., 1.]])
# Returns the upper triangular part of a matrix (2-D tensor), the other elements of the result tensor out are set to 0
out = torch.triu(torch.ones(5, 5))
print(out)
# tensor([[1., 1., 1., 1., 1.],
# [0., 1., 1., 1., 1.],
# [0., 0., 1., 1., 1.],
# [0., 0., 0., 1., 1.],
# [0., 0., 0., 0., 1.]])
# Fills elements of self tensor with value, -inf where mask is True
out = torch.zeros(5, 5).masked_fill(torch.tril(torch.ones(5, 5)) == 0, float('-inf'))
print(out)
# tensor([[0., -inf, -inf, -inf, -inf],
# [0., 0., -inf, -inf, -inf],
# [0., 0., 0., -inf, -inf],
# [0., 0., 0., 0., -inf],
# [0., 0., 0., 0., 0.]])
# Returns a tensor that is a transposed version of input wheret the given dimensions dim0 and dim1 are swapped
input = torch.zeros(2, 3, 4)
out = input.transpose(0, 2)
print(out.shape)
print(out)
# torch.Size([4, 3, 2])
# tensor([[[0., 0.],
# [0., 0.],
# [0., 0.]],
#
# [[0., 0.],
# [0., 0.],
# [0., 0.]],
#
# [[0., 0.],
# [0., 0.],
# [0., 0.]],
#
# [[0., 0.],
# [0., 0.],
# [0., 0.]]])
Linear Transformations
The linear layer in PyTorch applies an affine transformation, represented as \( y = xA^T + b \), where \( y \) is the output, \( x \) is the input, \( A \) is the weight matrix and \( b \) is the bias vector.
import torch.nn as nn
sample = torch.tensor([10., 10., 10.])
linear = nn.Linear(3, 3, bias=False)
print(linear)
print(linear(sample))
# Output: tensor([10., 10., 10.])
# tensor([-0.8503, -5.8184, 1.0190], grad_fn=<SqueezeBackward4>)
Softmax
The softmax function rescales an input tensor so its elements lie between 0 and 1 and sum to 1. Softmax is defined as:
$$ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}} $$and \( e \) is a mathematical constant, where \( e \approx 2.71828 \).
import torch.nn.functional as F
tensor1 = torch.tensor([1.0, 2.0, 3.0])
softmax_output = F.softmax(tensor1, dim=0)
print(softmax_output)
# Output: tensor([0.0900, 0.2447, 0.6652])
Embedding
An embedding layer stores dense representations of a fixed dictionary of words or indices.
# Initialize an embedding layer
vocab_size = 80
embedding_dim = 6
embedding = nn.Embedding(vocab_size, embedding_dim)
# Create some input indices
input_indices = torch.LongTensor([1, 5, 3, 2])
print(input_indices)
# Apply the embedding layer
embedded_output = embedding(input_indices)
# The output will be a tensor of shape (4, 6), where 4 is the number of inputs
# and 6 is the dimensionality of the embedding vectors
print(embedded_output.shape)
torch.Size([4, 6])
# tensor([[ 1.1766, 1.3491, -0.2536, 0.5023, 0.4930, 0.3043],
# [ 0.3194, 1.2871, 0.5535, 0.7847, -0.1497, 0.6422],
# [-1.0683, 1.6570, 0.3645, -1.2519, 2.5594, -1.0523],
# [ 1.4452, -0.2749, 0.7373, 0.4051, -0.4702, -1.2839]],
# grad_fn=<EmbeddingBackward0>)
Activation Functions: Sigmoid and GELU
Sigmoid
Sigmoid squashes the input into a range between 0 and 1. It is defined as:
$$ \sigma(x) = \frac{1}{1 + e^x} $$m = nn.Sigmoid()
input = torch.randn(2)
output = m(input)
print(input)
print(output)
# tensor([ 0.8731, -0.2994])
# tensor([0.7054, 0.4257])
GELU
GELU (Gaussian Error Linear Units) provides smoother activation, which can enhance model performance. It is defined as:
$$ \text{GELU}(x) = x \cdot \Phi(x) $$m = nn.GELU()
input = torch.randn(2)
output = m(input)
print(input)
print(output)
# tensor([-0.4450, -0.4593])
# tensor([-0.1460, -0.1484])
Broadcasting semantics
PyTorch operations often support NumPy-style broadcasting, where tensor arguments expand to equal sizes automatically without copying data.
x = torch.tensor([1, 2, 3])
print(x.shape)
y = torch.tensor([[1], [2], [3]])
print(y.shape)
(x+y).size()
# torch.Size([3])
# torch.Size([3, 1])
# torch.Size([3, 3])
Standard Deviation
The standard deviation \( (\sigma) \) of a dataset \( X = \{x_1, x_2, \ldots, x_n\} \) is calculated as:
$$ \sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2} $$This value indicates the average deviation of the data points from the mean, providing insight into the dataset’s spread.
import numpy as np
data = np.array([2, 4, 4, 4, 5, 5, 7, 9])
mean = np.mean(data)
print(mean)
squared_diff = (data - mean) ** 2
print(squared_diff)
sum_squared_diff = np.sum(squared_diff)
print(sum_squared_diff)
n = len(data)
variance = sum_squared_diff / n
std_dev = np.sqrt(variance)
print(std_dev)
# Output:
# Mean: 5.0
# Square Differences: [ 9. 1. 1. 1. 0. 0. 4. 16.]
# Sum of Squared Differences: 32.0
# Standard Deviation: 2.0
Reproducing GPT-2 from Scratch
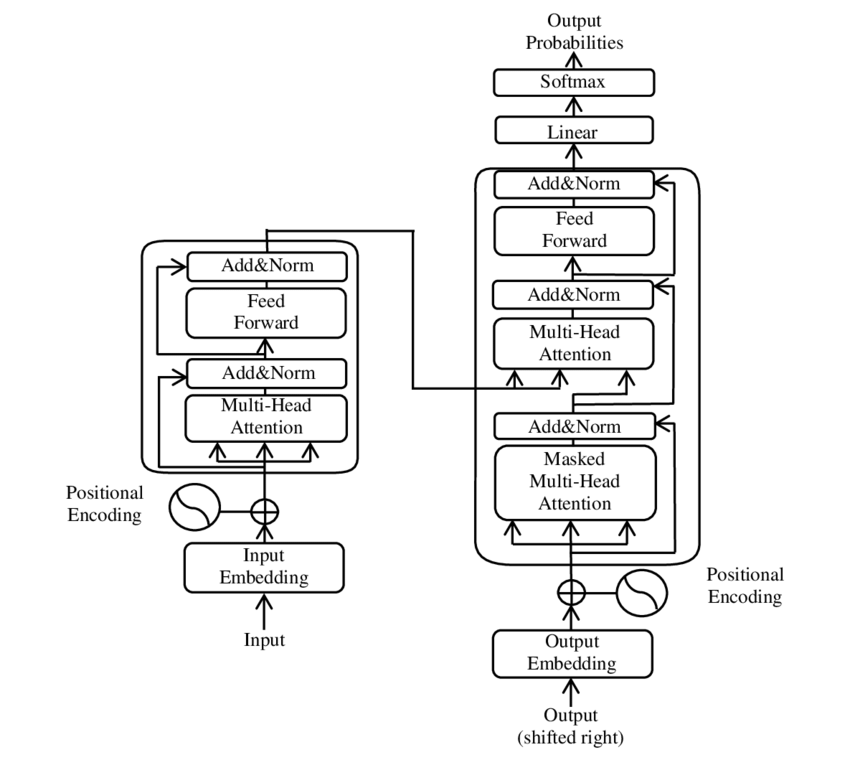
After successfully navigating the transformer fundamentals, I took on another challenge with Andrej Karpathy’s four-hour tutorial Let’s reproduce GPT-2(124M). This section guides you through the model-building and weights-initialization process, and contrasts with the original architecture presented in the landmark paper Attention Is All You Need, which combines encoder and decoder components. GPT-2, however, only utilizes the decoder segment, making it unique in structure and application.
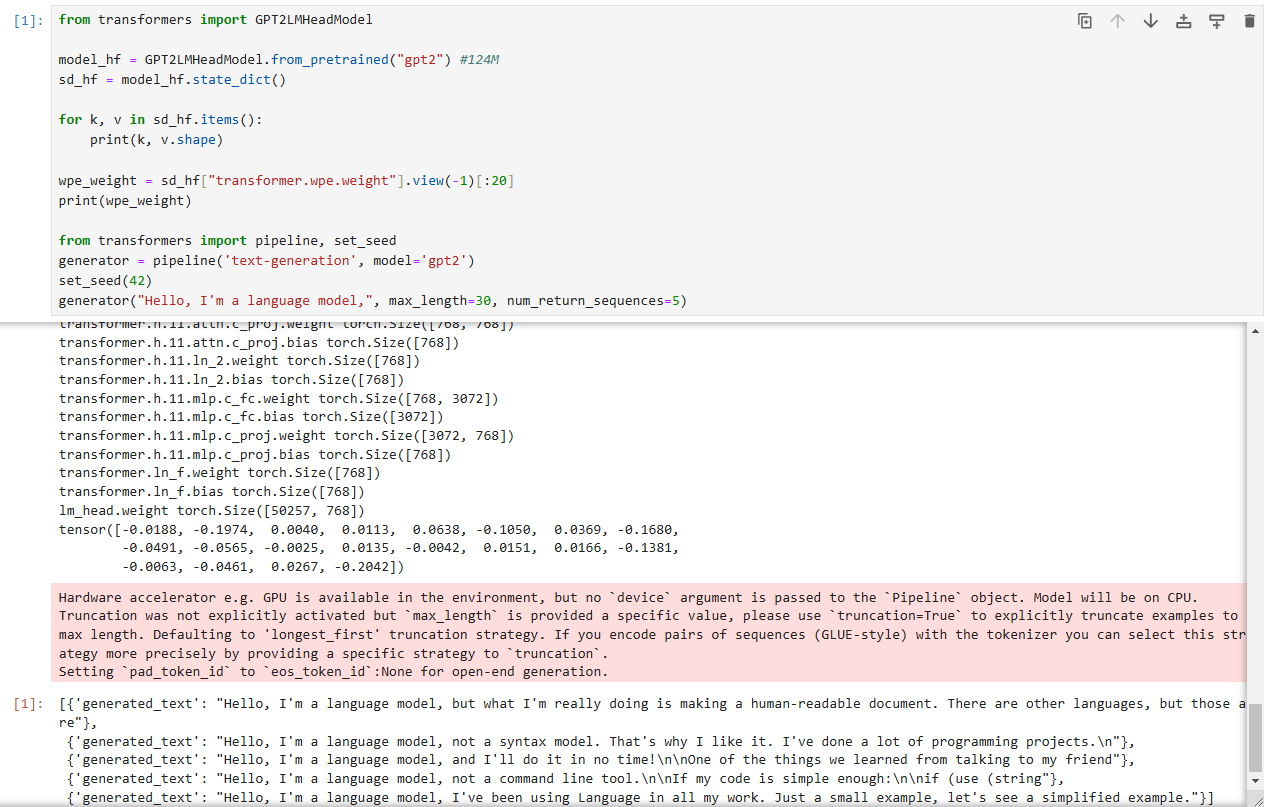
Loading Pretrained GPT-2 Weights
The initial part of the tutorial goes over setting up a pretrained GPT-2 model using the transformers library, allowing us to see how the model behaves with the pretrained weights. Here’s the example provided by Andrej Karpathy, to initiate GPT-2 and generate text based on an input prompt:
from transformers import GPT2LMHeadModel
model_hf = GPT2LMHeadModel.from_pretrained("gpt2") #124M
sd_hf = model_hf.state_dict()
for k, v in sd_hf.items():
print(k, v.shape)
wpe_weight = sd_hf["transformer.wpe.weight"].view(-1)[:20]
print(wpe_weight)
from transformers import pipeline, set_seed
generator = pipeline('text-generation', model='gpt2')
set_seed(42)
generator("Hello, I'm a language model,", max_length=30, num_return_sequences=5)
This helped in understanding how the weights are structured and provides a baseline for further model modifications.
Building GPT-2 from Scratch
Following the analysis of pretrained weights, Andrej Karpathy started constructing the model from the ground up. The main class includes components like CausalSelfAttention, which handles the attention mechanism, and a simple MLP layer to process the embeddings.
Here’s a snippet of the core setup, where each block layer is defined, and the pretrained weights are loaded into the model for text generation:
- The initialization:
from dataclasses import dataclass
import torch
import torch.nn as nn
from torch.nn import functional as F
import math
- The main GPT class, using the pretrained gpt2 (124M) weights:
class CausalSelfAttention(nn.Module):
def __init__(self, config):
super().__init__()
assert config.n_embd % config.n_head == 0
# key, query, value projections for all heads, but in a batch
self.c_attn = nn.Linear(config.n_embd, 3 * config.n_embd)
# output projection
self.c_proj = nn.Linear(config.n_embd, config.n_embd)
# regularization
self.n_head = config.n_head
self.n_embd = config.n_embd
self.register_buffer("bias", torch.tril(torch.ones(config.block_size, config.block_size))
.view(1, 1, config.block_size, config.block_size))
def forward(self, x):
B, T, C = x.size() # batch size, sequence length, embedding dimensionality (n_embd)
qkv = self.c_attn(x)
q, k, v = qkv.split(self.n_embd, dim=2)
k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
att = F.softmax(att, dim=-1)
y = att @ v # (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
y = y.transpose(1, 2).contiguous().view(B, T, C) # re-assemble all head outputs side by side
# output projection
y = self.c_proj(y)
return y
class MLP(nn.Module):
def __init__(self, config):
super().__init__()
self.c_fc = nn.Linear(config.n_embd, 4 * config.n_embd)
self.gelu = nn.GELU(approximate='tanh')
self.c_proj = nn.Linear(4 * config.n_embd, config.n_embd)
def forward(self, x):
x = self.c_fc(x)
x = self.gelu(x)
x = self.c_proj(x)
return x
class Block(nn.Module):
def __init__(self, config):
super().__init__()
self.ln_1 = nn.LayerNorm(config.n_embd)
self.attn = CausalSelfAttention(config)
self.ln_2 = nn.LayerNorm(config.n_embd)
self.mlp = MLP(config)
def forward(self, x):
x = x + self.attn(self.ln_1(x))
x = x + self.mlp(self.ln_2(x))
return x
@dataclass
class GPTConfig:
block_size: int = 1024
vocab_size: int = 50257
n_layer: int = 12
n_head: int = 12
n_embd: int = 768
class GPT(nn.Module):
def __init__(self, config):
super().__init__()
self.config = config
self.transformer = nn.ModuleDict(dict(
wte = nn.Embedding(config.vocab_size, config.n_embd),
wpe = nn.Embedding(config.block_size, config.n_embd),
h = nn.ModuleList([Block(config) for _ in range(config.n_layer)]),
ln_f = nn.LayerNorm(config.n_embd),
))
self.lm_head = nn.Linear(config.n_embd, config.vocab_size, bias=False)
def forward(self, idx):
B, T = idx.size()
assert T <= self.config.block_size, f"Cannot forward sequence of length {t}, block size is only {self.config.block_size}"
pos = torch.arange(0, T, dtype=torch.long, device=idx.device) # shape (t)
pos_emb = self.transformer.wpe(pos) # position embeddings of shape (t, n_embd)
tok_emb = self.transformer.wte(idx) # token embeddings of shape (b, t, n_embd)
x = tok_emb + pos_emb
for block in self.transformer.h:
x = block(x)
x = self.transformer.ln_f(x)
logits = self.lm_head(x)
return logits
@classmethod
def from_pretrained(cls, model_type):
assert model_type in {'gpt2', 'gpt2-medium', 'gpt2-large', 'gpt2-xl'}
from transformers import GPT2LMHeadModel
print("loading weights from pretrained gpt: %s" % model_type)
# n_layer, n_head and n_embd are determined from model_type
config_args = {
'gpt2': dict(n_layer=12, n_head=12, n_embd=768), # 124M params
'gpt2-medium': dict(n_layer=24, n_head=16, n_embd=1024), # 350M params
'gpt2-large': dict(n_layer=36, n_head=20, n_embd=1280), # 774M params
'gpt2-xl': dict(n_layer=48, n_head=25, n_embd=1600), # 1558M params
}[model_type]
config_args['vocab_size'] = 50257 # always 50257 for GPT model checkpoints
config_args['block_size'] = 1024 # always 1024 for GPT model checkpoints
# create a from-scratch initialized minGPT model
config = GPTConfig(**config_args)
model = GPT(config)
sd = model.state_dict()
sd_keys = sd.keys()
sd_keys = [k for k in sd_keys if not k.endswith('.attn.bias')] # discard this mask / buffer, not a param
# init a huggingface/transformers model
model_hf = GPT2LMHeadModel.from_pretrained(model_type)
sd_hf = model_hf.state_dict()
# copy while ensuring all of the parameters are aligned and match in names and shapes
sd_keys_hf = sd_hf.keys()
sd_keys_hf = [k for k in sd_keys_hf if not k.endswith('.attn.masked_bias')] # ignore these, just a buffer
sd_keys_hf = [k for k in sd_keys_hf if not k.endswith('.attn.bias')] # same, just the mask (buffer)
transposed = ['attn.c_attn.weight', 'attn.c_proj.weight', 'mlp.c_fc.weight', 'mlp.c_proj.weight']
# basically the openai checkpoints use a "Conv1D" module, but we only want to use a vanilla Linear
# this means that we have to transpose these weights when we import them
assert len(sd_keys_hf) == len(sd_keys), f"mismatched keys: {len(sd_keys_hf)} != {len(sd_keys)}"
for k in sd_keys_hf:
if any(k.endswith(w) for w in transposed):
# special treatment for the Conv1D weights we need to transpose
assert sd_hf[k].shape[::-1] == sd[k].shape, f"Shape mismatch for {k}: {sd_hf[k].shape[::-1]} vs {sd[k].shape}"
with torch.no_grad():
sd[k].copy_(sd_hf[k].t())
else:
# vanilla copy over the other parameters
assert sd_hf[k].shape == sd[k].shape, f"Shape mismatch for {k}: {sd_hf[k].shape} vs {sd[k].shape}"
with torch.no_grad():
sd[k].copy_(sd_hf[k])
return model
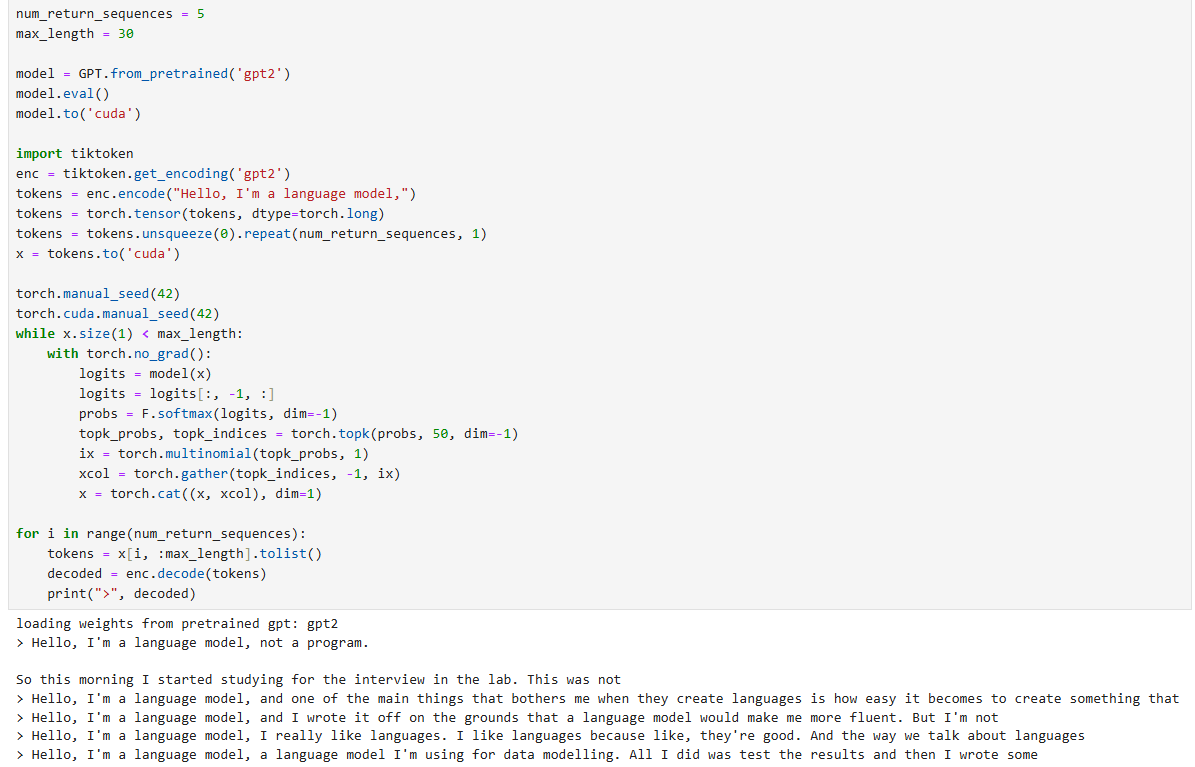
- Text generation for the main GPT class using the pretrained weights:
num_return_sequences = 5
max_length = 30
model = GPT.from_pretrained('gpt2')
model.eval()
model.to('cuda')
import tiktoken
enc = tiktoken.get_encoding('gpt2')
tokens = enc.encode("Hello, I'm a language model,")
tokens = torch.tensor(tokens, dtype=torch.long)
tokens = tokens.unsqueeze(0).repeat(num_return_sequences, 1)
x = tokens.to('cuda')
torch.manual_seed(42)
torch.cuda.manual_seed(42)
while x.size(1) < max_length:
with torch.no_grad():
logits = model(x)
logits = logits[:, -1, :]
probs = F.softmax(logits, dim=-1)
topk_probs, topk_indices = torch.topk(probs, 50, dim=-1)
ix = torch.multinomial(topk_probs, 1)
xcol = torch.gather(topk_indices, -1, ix)
x = torch.cat((x, xcol), dim=1)
for i in range(num_return_sequences):
tokens = x[i, :max_length].tolist()
decoded = enc.decode(tokens)
print(">", decoded)
Wrapping Up the Pretrained Model Setup
In this post, we’ve explored the foundational setup for loading pretrained GPT-2 weights and performing basic text generation. From analyzing the pretrained model structure to initializing and modifying key parameters, this approach sets the stage for a deeper dive into the intricacies of GPT-2. We’ve also covered the essentials for leveraging existing weights to understand and test the model’s capabilities.
In the next part, we’ll continue following Andrej Karpathy’s video as he takes the GPT-2 model through hands-on training with actual datasets. We’ll start with a small sample text to see the practical aspects of text generation training, followed by scaling to larger datasets.
Optional - Generate Model from Scratch
To create a model entirely from scratch, we can leverage PyTorch’s default random initialization rather than loading GPT-2’s pretrained weights.
The only modification needed in the configuration is as follows:
# model = GPT.from_pretrained('gpt2')
model = GPT(GPTConfig())
This setup will allow us to train a randomly initialized GPT model, shown below.
