From Routing Models to MIP: Solving Capacitated Vehicle Routing Problem

June 1, 2024 - 13 mins read

Series: Combinatorial Optimization Problems

Problem Statement

In this post, I will follow the Vehicle Routing Problem (VRP) with a focus on the capacitated vehicle routing problem (CVRP) and utilizing an alternative Mixed Integer Programming (MIP) approach.

Routing Model

The main section of the program creates the index manager and the routing model.

// Create Routing Index Manager
RoutingIndexManager manager = new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);

// Create Routing Model
RoutingModel routing = new RoutingModel(manager);

Distance Callback

The code snippet initializes the transit callback to compute distances between nodes and sets up the arc costs for all vehicles in the VRP model to ensure that the solver considers the correct distances when optimizing the routes:

// Create and register a transit callback
final int transitCallbackIndex =
    routing.registerTransitCallback((long fromIndex, long toIndex) -> {
        // Convert from routing variable Index to user NodeIndex.
        int fromNode = manager.indexToNode(fromIndex);
        int toNode = manager.indexToNode(toIndex);
        return (long) data.distanceMatrix[fromNode][toNode];
    });

// Define cost of each arc.
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);

Demand Callback and Capacity Constraints

The solver requires a demand callback, which returns the demand at each location, and a dimension for the vehicle capacity constraints:

// Add Capacity constraint.
final int demandCallbackIndex = routing.registerUnaryTransitCallback((long fromIndex) -> {
    // Convert from routing variable Index to user NodeIndex.
    int fromNode = manager.indexToNode(fromIndex);
    return data.demands[fromNode];
});
routing.addDimensionWithVehicleCapacity(demandCallbackIndex, 0, // null capacity slack
    data.vehicleCapacities, // vehicle maximum capacities
    true, // start cumul to zero
    "Capacity");

Changing the search strategy

Since the routing solver does not always return the optimal solution, we can use a more advanced search strategy called guided local search, which enables escaping a local minimum. We can further tune our use case with other Routing Options.

// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
    main.defaultRoutingSearchParameters()
        .toBuilder()
        .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
        .setLocalSearchMetaheuristic(LocalSearchMetaheuristic.Value.GUIDED_LOCAL_SEARCH)
        .setTimeLimit(Duration.newBuilder().setSeconds(60).build())
        .build();

Data Model

This is the data model:

@Data
@Builder
@AllArgsConstructor
@NoArgsConstructor
@Serdeable.Serializable
@Serdeable.Deserializable
public class DataModel {

    double[][] distanceMatrix;
    long[] demands;
    long[] vehicleCapacities;
    int vehicleNumber;
    int depot;

}

The CVRP Service

This is the Micronaut service for CVRP, with the printSolution method adapted from OR-Tools:

@Singleton
public class CVRPService {

    static {
        Loader.loadNativeLibraries();
    }

    CVRPSolution solve(DataModel data) {
        // Create Routing Index Manager
        RoutingIndexManager manager = new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);

        // Create Routing Model
        RoutingModel routing = new RoutingModel(manager);

        // Create and register a transit callback
        final int transitCallbackIndex =
                routing.registerTransitCallback((long fromIndex, long toIndex) -> {
                    // Convert from routing variable Index to user NodeIndex.
                    int fromNode = manager.indexToNode(fromIndex);
                    int toNode = manager.indexToNode(toIndex);
                    return (long) data.distanceMatrix[fromNode][toNode];
                });

        // Define cost of each arc.
        routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);

        // Add Capacity constraint.
        final int demandCallbackIndex = routing.registerUnaryTransitCallback((long fromIndex) -> {
            // Convert from routing variable Index to user NodeIndex.
            int fromNode = manager.indexToNode(fromIndex);
            return data.demands[fromNode];
        });
        routing.addDimensionWithVehicleCapacity(demandCallbackIndex, 0, // null capacity slack
                data.vehicleCapacities, // vehicle maximum capacities
                true, // start cumul to zero
                "Capacity");

        // Setting first solution heuristic.
        RoutingSearchParameters searchParameters =
                main.defaultRoutingSearchParameters()
                        .toBuilder()
                        .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
                        .setLocalSearchMetaheuristic(LocalSearchMetaheuristic.Value.GUIDED_LOCAL_SEARCH)
                        .setTimeLimit(Duration.newBuilder().setSeconds(60).build())
                        .build();

        // Solve the problem.
        Assignment solution = routing.solveWithParameters(searchParameters);

        Map<Integer, String> vehicleMap = new HashMap<>();
        for (int i = 0; i < data.vehicleNumber; ++i) {
            long index = routing.start(i);
            long routeLoad = 0;
            String route = "";
            while (!routing.isEnd(index)) {
                long nodeIndex = manager.indexToNode(index);
                routeLoad += data.demands[(int) nodeIndex];
                route += nodeIndex + " Load(" + routeLoad + ") -> ";
                long previousIndex = index;
                index = solution.value(routing.nextVar(index));
            }
            route += manager.indexToNode(routing.end(i));
            vehicleMap.put(i, route);
        }

        return CVRPSolution.builder().objectiveValue(solution.objectiveValue()).variableValue(vehicleMap).build();
    }

}

The CVRP Controller

Here is the Micronaut controller for the CVRP:

@Controller("/cvrp")
public class CVRPController {

    private final CVRPService cvrpService;

    public CVRPController(CVRPService cvrpService) {
        this.cvrpService = cvrpService;
    }

    @Post("/solve")
    @Produces(MediaType.APPLICATION_JSON)
    @Consumes(MediaType.APPLICATION_JSON)
    public CVRPSolution solve(@Body DataModel dataModel) {
        return cvrpService.solve(dataModel);
    }

}

The Input

This is the sample input from the OR-Tools:

{
    "distanceMatrix": [
        [0, 548, 776, 696, 582, 274, 502, 194, 308, 194, 536, 502, 388, 354, 468, 776, 662],
        [548, 0, 684, 308, 194, 502, 730, 354, 696, 742, 1084, 594, 480, 674, 1016, 868, 1210],
        [776, 684, 0, 992, 878, 502, 274, 810, 468, 742, 400, 1278, 1164, 1130, 788, 1552, 754],
        [696, 308, 992, 0, 114, 650, 878, 502, 844, 890, 1232, 514, 628, 822, 1164, 560, 1358],
        [582, 194, 878, 114, 0, 536, 764, 388, 730, 776, 1118, 400, 514, 708, 1050, 674, 1244],
        [274, 502, 502, 650, 536, 0, 228, 308, 194, 240, 582, 776, 662, 628, 514, 1050, 708],
        [502, 730, 274, 878, 764, 228, 0, 536, 194, 468, 354, 1004, 890, 856, 514, 1278, 480],
        [194, 354, 810, 502, 388, 308, 536, 0, 342, 388, 730, 468, 354, 320, 662, 742, 856],
        [308, 696, 468, 844, 730, 194, 194, 342, 0, 274, 388, 810, 696, 662, 320, 1084, 514],
        [194, 742, 742, 890, 776, 240, 468, 388, 274, 0, 342, 536, 422, 388, 274, 810, 468],
        [536, 1084, 400, 1232, 1118, 582, 354, 730, 388, 342, 0, 878, 764, 730, 388, 1152, 354],
        [502, 594, 1278, 514, 400, 776, 1004, 468, 810, 536, 878, 0, 114, 308, 650, 274, 844],
        [388, 480, 1164, 628, 514, 662, 890, 354, 696, 422, 764, 114, 0, 194, 536, 388, 730],
        [354, 674, 1130, 822, 708, 628, 856, 320, 662, 388, 730, 308, 194, 0, 342, 422, 536],
        [468, 1016, 788, 1164, 1050, 514, 514, 662, 320, 274, 388, 650, 536, 342, 0, 764, 194],
        [776, 868, 1552, 560, 674, 1050, 1278, 742, 1084, 810, 1152, 274, 388, 422, 764, 0, 798],
        [662, 1210, 754, 1358, 1244, 708, 480, 856, 514, 468, 354, 844, 730, 536, 194, 798, 0]
    ],
    "demands":[0, 1, 1, 2, 4, 2, 4, 8, 8, 1, 2, 1, 2, 4, 4, 8, 8],
    "vehicleCapacities":[15, 15, 15, 15],
    "vehicleNumber":4,
    "depot" :0
}

The CVRPSolution

This is the CVRPSolution:

@Data
@Builder
@AllArgsConstructor
@NoArgsConstructor
@Serdeable.Serializable
public class CVRPSolution {

    private double objectiveValue;
    private Map<Integer, String> variableValue;

}

Solver in Action

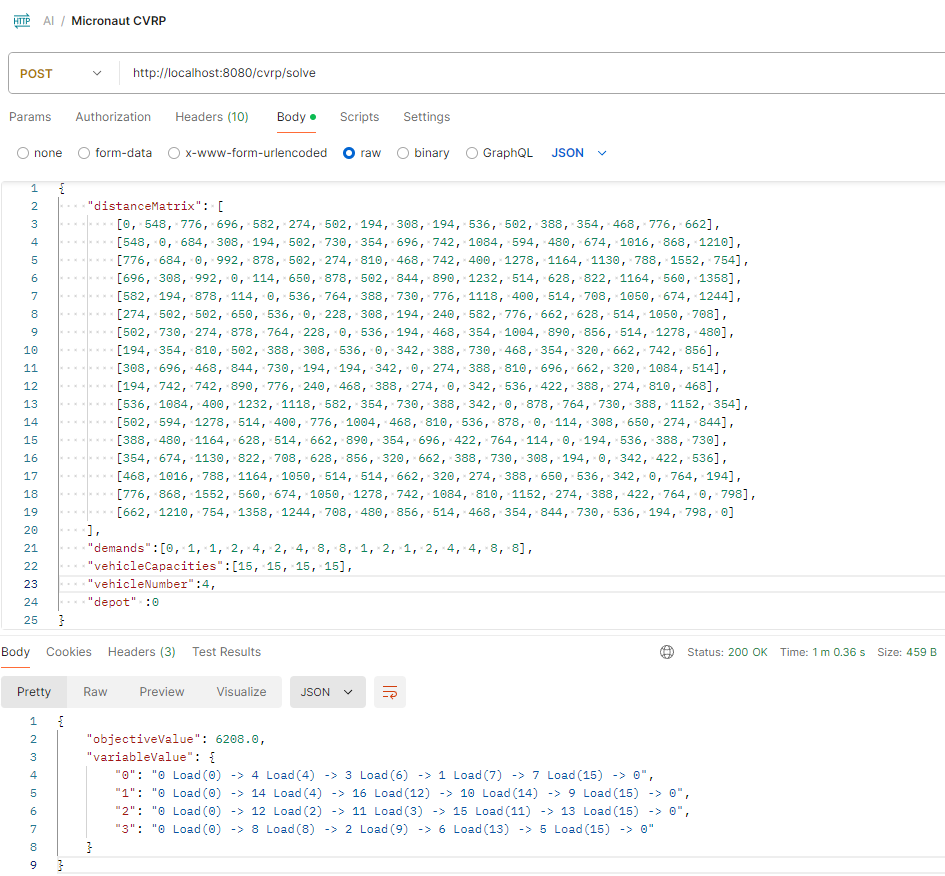
cvrp-micronaut-postman-result

Optional: Solving using MIP Approach

Let’s create a solveMIP method in CVRPService.java:

// Create the MIP solver
MPSolver solver = new MPSolver("CVRP", MPSolver.OptimizationProblemType.CBC_MIXED_INTEGER_PROGRAMMING);

Variables

Let $ t $ be the decision variable for denoting that vehicle $ k $ will travel from node $ i $ to node $ j $. Let $ s $ be the decision variable for denoting that node $ i $ is fulfilled by vehicle $ k $.

// Variables: t[i][j][k] is 1 if vehicle k travels from node i to node j
MPVariable[][][] t = new MPVariable[numNodes][numNodes][numVehicles];
for (int i = 0; i < numNodes; i++) {
    for (int j = 0; j < numNodes; j++) {
        if (i != j) {
            for (int k = 0; k < numVehicles; k++) {
                t[i][j][k] = solver.makeIntVar(0, 1, "travel_" + i + "_" + j + "_" + k);
            }
        }
    }
}

// Variables: s[i][k] is 1 if node i is fulfilled by k
MPVariable[][] s = new MPVariable[numNodes][numVehicles];
for (int i = 0; i < numNodes; i++) {
    for (int k = 0; k < numVehicles; k++) {
        s[i][k] = solver.makeIntVar(0, 1, "serve_" + i + "_" + k);
    }
}

Objectives

Minimize the total distance travelled by all vehicles:

$$ \sum_{k \in K} \sum_{i \in I} \sum_{j \in J} t_{i,j,k} \cdot \text{{distance matrix}}_{i,j} $$

This is implemented as:

// Objective: Minimize the total distance traveled
MPObjective objective = solver.objective();
for (int k = 0; k < numVehicles; k++) {
    for (int i = 0; i < numNodes; i++) {
        for (int j = 0; j < numNodes; j++) {
            if (i != j) {
                objective.setCoefficient(t[i][j][k],  data.distanceMatrix[i][j]);
            }
        }
    }
}
objective.setMinimization();

Constraints

Each vehicle starts at the depot:

$$ \sum_{j} t_{0,j,k} = 1 \quad \forall k $$

Each vehicle ends at the depot:

$$ \sum_{i} t_{i,0,k} = 1 \quad \forall k $$

This is implemented as:

// 1. Each vehicle starts at the depot
for (int k = 0; k < numVehicles; k++) {
    MPConstraint constraint = solver.makeConstraint(1, 1, "depot_start_" + k);
    for (int j = 1; j < numNodes; j++) {
        constraint.setCoefficient(t[depot][j][k], 1);
    }
}

// 2. Each vehicle ends at the depot
for (int k = 0; k < numVehicles; k++) {
    MPConstraint constraint = solver.makeConstraint(1, 1, "deport_end_" + k);
    for (int i = 1; i < numNodes; i++) {
        constraint.setCoefficient(t[i][depot][k], 1);
    }
}

Each Node Is Visited Exactly Once by Exactly One Vehicle (Excluding Depot):

$$ \sum_{i \neq j} x_{i,j,k} = 1 \quad \forall j $$

This is implemented as:

// 3. Each node is visited exactly once by exactly one vehicle (excluding depot)
for (int j = 1; j < numNodes; j++) {
    MPConstraint constraint = solver.makeConstraint(1, 1, "visit_node_" + j);
    for (int i = 0; i < numNodes; i++) {
        if (i != j) {
            for (int k = 0; k < numVehicles; k++) {
                constraint.setCoefficient(t[i][j][k], 1);
            }
        }
    }
}

Flow Conservation: If a vehicle arrives at a node, it must leave:

$$ \sum_{\substack{i \neq n}} t_{i,n,k} - \sum_{\substack{j \neq n}} t_{n,j,k} = 0, \quad \forall n, k $$

This is implemented as:

// 4. Flow conservation: if a vehicle arrives at a node, it must leave
for (int k = 0; k < numVehicles; k++) {
    for (int n = 0; n < numNodes; n++) {  // Include depot to enforce return
        MPConstraint constraint = solver.makeConstraint(0, 0, "flow_conservation_" + n + "_" + k);
        for (int i = 0; i < numNodes; i++) {
            if (i != n) {
                constraint.setCoefficient(t[i][n][k], 1);
            }
        }
        for (int j = 0; j < numNodes; j++) {
            if (n != j) {
                constraint.setCoefficient(t[n][j][k], -1);
            }
        }
    }
}

Capacity constraints: For each vehicle $k $, ensure that the total demand on its route does not exceed its capacity:

$$ \sum_{i \neq j} t_{i,j,k} \cdot \text{{demand}}_i \leq \text{{vehicle capacity}}_k \quad \forall k $$

This is implemented as:

// 5. Capacity constraints
for (int k = 0; k < numVehicles; k++) {
    MPConstraint constraint = solver.makeConstraint(0, data.vehicleCapacities[k], "capacity_" + k);
    for (int i = 1; i < numNodes; i++) {
        for (int j = 1; j < numNodes; j++) {
            if (i != j) {
                constraint.setCoefficient(t[i][j][k], data.demands[i]);
            }
        }
    }
}

Subtour elimination constraints: To ensure that there are no subtours (sub-routes) in the solution, we introduce auxiliary variables $ 𝑢 $ for each customer node $ i $. These variables help enforce the sequence in which nodes are visited, preventing isolated cycles that do not include the depot. Ths subtour elimination constraint is given by:

$$ u_i - u_j + M \cdot t_{i,j,k} \leq M - 1, \quad \forall i \neq j, \forall k $$

This is implemented as:

// Create auxiliary variables for subtour elimination
MPVariable[] u = new MPVariable[numNodes];
for (int i = 1; i < numNodes; i++) {
    u[i] = solver.makeIntVar(0, numNodes, "u_" + i);
}

// 6. Subtour elimination constraints
for (int k = 0; k < numVehicles; k++) {
    for (int i = 1; i < numNodes; i++) {
        for (int j = 1; j < numNodes; j++) {
            if (i != j) {
                MPConstraint subtourConstraint  = solver.makeConstraint(-MPSolver.infinity(), numNodes - 1, "subtour_elimination_" + i + "_" + j + "_" + k);
                subtourConstraint.setCoefficient(u[i], 1);
                subtourConstraint.setCoefficient(u[j], -1);
                subtourConstraint.setCoefficient(t[i][j][k], numNodes);
            }
        }
    }
}

Putting it together

This is the sovleMIP method in CVRPService.java:

CVRPSolution solveMIP(DataModel data) {
    final int numNodes = data.distanceMatrix.length;
    final int numVehicles = data.vehicleNumber;
    final int depot = data.depot;

    // Create the MIP solver
    MPSolver solver = new MPSolver("CVRP", MPSolver.OptimizationProblemType.CBC_MIXED_INTEGER_PROGRAMMING);

    // Variables: t[i][j][k] is 1 if vehicle k travels from node i to node j
    MPVariable[][][] t = new MPVariable[numNodes][numNodes][numVehicles];
    for (int i = 0; i < numNodes; i++) {
        for (int j = 0; j < numNodes; j++) {
            if (i != j) {
                for (int k = 0; k < numVehicles; k++) {
                    t[i][j][k] = solver.makeIntVar(0, 1, "travel_" + i + "_" + j + "_" + k);
                }
            }
        }
    }

    // Variables: s[i][k] is 1 if node i is served by k
    MPVariable[][] s = new MPVariable[numNodes][numVehicles];
    for (int i = 0; i < numNodes; i++) {
        for (int k = 0; k < numVehicles; k++) {
            s[i][k] = solver.makeIntVar(0, 1, "serve_" + i + "_" + k);
        }
    }

    // Objective: Minimize the total distance traveled
    MPObjective objective = solver.objective();
    for (int k = 0; k < numVehicles; k++) {
        for (int i = 0; i < numNodes; i++) {
            for (int j = 0; j < numNodes; j++) {
                if (i != j) {
                    objective.setCoefficient(t[i][j][k],  data.distanceMatrix[i][j]);
                }
            }
        }
    }
    objective.setMinimization();

    // Constraints:
    // 1. Each vehicle starts at the depot
    for (int k = 0; k < numVehicles; k++) {
        MPConstraint constraint = solver.makeConstraint(1, 1, "depot_start_" + k);
        for (int j = 1; j < numNodes; j++) {
            constraint.setCoefficient(t[depot][j][k], 1);
        }
    }

    // 2. Each vehicle ends at the depot
    for (int k = 0; k < numVehicles; k++) {
        MPConstraint constraint = solver.makeConstraint(1, 1, "deport_end_" + k);
        for (int i = 1; i < numNodes; i++) {
            constraint.setCoefficient(t[i][depot][k], 1);
        }
    }

    // 3. Each node is visited exactly once by exactly one vehicle (excluding depot)
    for (int j = 1; j < numNodes; j++) {
        MPConstraint constraint = solver.makeConstraint(1, 1, "visit_node_" + j);
        for (int i = 0; i < numNodes; i++) {
            if (i != j) {
                for (int k = 0; k < numVehicles; k++) {
                    constraint.setCoefficient(t[i][j][k], 1);
                }
            }
        }
    }

    // 4. Flow conservation: if a vehicle arrives at a node, it must leave
    for (int k = 0; k < numVehicles; k++) {
        for (int n = 0; n < numNodes; n++) {  // Include depot to enforce return
            MPConstraint constraint = solver.makeConstraint(0, 0, "flow_conservation_" + n + "_" + k);
            for (int i = 0; i < numNodes; i++) {
                if (i != n) {
                    constraint.setCoefficient(t[i][n][k], 1);
                }
            }
            for (int j = 0; j < numNodes; j++) {
                if (n != j) {
                    constraint.setCoefficient(t[n][j][k], -1);
                }
            }
        }
    }

    // 5. Capacity constraints
    for (int k = 0; k < numVehicles; k++) {
        MPConstraint constraint = solver.makeConstraint(0, data.vehicleCapacities[k], "capacity_" + k);
        for (int i = 1; i < numNodes; i++) {
            for (int j = 1; j < numNodes; j++) {
                if (i != j) {
                    constraint.setCoefficient(t[i][j][k], data.demands[i]);
                }
            }
        }
    }

    // Create auxiliary variables for subtour elimination
    MPVariable[] u = new MPVariable[numNodes];
    for (int i = 1; i < numNodes; i++) {
        u[i] = solver.makeIntVar(0, numNodes, "u_" + i);
    }

    // 6. Subtour elimination constraints
    for (int k = 0; k < numVehicles; k++) {
        for (int i = 1; i < numNodes; i++) {
            for (int j = 1; j < numNodes; j++) {
                if (i != j) {
                    MPConstraint subtourConstraint  = solver.makeConstraint(-MPSolver.infinity(), numNodes - 1, "subtour_elimination_" + i + "_" + j + "_" + k);
                    subtourConstraint.setCoefficient(u[i], 1);
                    subtourConstraint.setCoefficient(u[j], -1);
                    subtourConstraint.setCoefficient(t[i][j][k], numNodes);
                }
            }
        }
    }

    // Solve
    solver.setTimeLimit(10000);
    MPSolver.ResultStatus resultStatus = solver.solve();

    // Check the result
    Map<Integer, String> vehicleMap = new HashMap<>();

    if (resultStatus == MPSolver.ResultStatus.OPTIMAL || resultStatus == MPSolver.ResultStatus.FEASIBLE) {
        for (int k = 0; k < numVehicles; k++) {
            int currentNode = depot;
            String route = String.valueOf(depot);  // Start from the depot
            while (true) {
                boolean routeContinues = false;
                for (int j = 0; j < numNodes; j++) {
                    if (currentNode != j && t[currentNode][j][k].solutionValue() == 1.0) {
                        route += " -> " + j;
                        currentNode = j;
                        routeContinues = true;
                        break;
                    }
                }
                if (!routeContinues || currentNode == depot) {
                    break;  // No further route found for this vehicle
                }
            }
            vehicleMap.put(k, route);
        }
    }
    return CVRPSolution.builder().objectiveValue(objective.value()).variableValue(vehicleMap).build();
}

The updated controller

This is the refactored CVRPController.java:

@Post("/solveMIP")
@Produces(MediaType.APPLICATION_JSON)
@Consumes(MediaType.APPLICATION_JSON)
public CVRPSolution solveMIP(@Body DataModel dataModel) {
    return cvrpService.solveMIP(dataModel);
}

MIP Solver in Action

This is the result for the sample data:

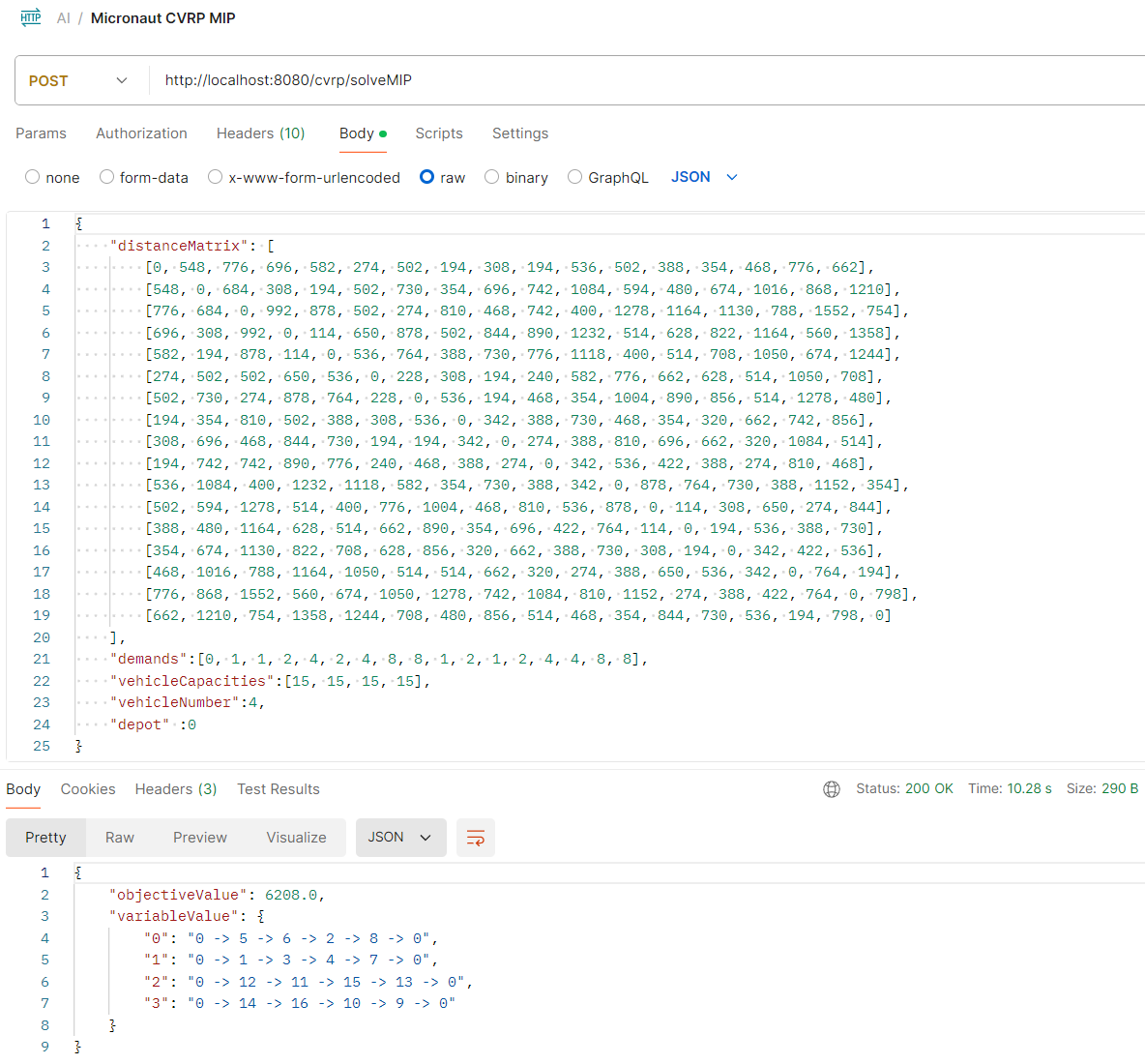
cvrp-mip-micronaut-postman-result

The MIP approach provides a precise method for solving the Capacitated Vehicle Routing Problem, offering optimal solutions but with higher computational demands. This makes it less suitable for very large instances or real-time applications compared to heuristic methods. While MIP handles complex constraints more flexibly, traditional routing models are faster and more scalable. Therefore, the choice between MIP and traditional methods depends on the problem’s requirements, such as accuracy, size, and available computational resources. MIP remains a powerful tool for tackling challenging optimization problems in logistics and transportation.

This is a post in the Combinatorial Optimization Problems series.
Other posts in this series:

June 1, 2024 - From Routing Models to MIP: Solving Capacitated Vehicle Routing Problem
May 27, 2024 - Solving Facility Location Problem with OR-Tools and Micronaut
May 23, 2024 - Optimizing TSP with Genetic Algorithms in Micronaut
April 27, 2024 - Efficient TSP Solver API with Micronaut