Problem Statement
I’m embarking on a journey to solve the Travelling Salesman Problem (TSP) utilizing Choco-solver, an effective Java library for constraint programming. Additionally, I’ll be converting this solution into an API using Micronaut, a cutting-edge, JVM-based framework for building modular, testable microservices and serverless applications.
Setting up with Micronaut
Following the official Micronaut guide, I downloaded the source and proceeded with the setup.
Dependencies Configuration
I made adjustments to the dependencies in the build.gradle file to incorporate necessary libraries such as log4j, Lombok annotations, and Choco-solver.
dependencies {
annotationProcessor("io.micronaut:micronaut-http-validation")
annotationProcessor("io.micronaut.serde:micronaut-serde-processor")
annotationProcessor("org.projectlombok:lombok")
implementation("org.projectlombok:lombok")
implementation("org.slf4j:slf4j-api")
implementation("io.micronaut.serde:micronaut-serde-jackson")
implementation("org.choco-solver:choco-solver:4.10.14")
compileOnly("io.micronaut:micronaut-http-client")
runtimeOnly("ch.qos.logback:logback-classic")
testImplementation("io.micronaut:micronaut-http-client")
}
Running micronaut
By running the gradle task from Intellij or via command line, .\gradlew run, this will be the expected result:
Working on the TSPSolver
Input Definition
In the TSPSolver.java, I began by defining the inputs required for the solver. This includes setting up variables to represent the tour, distances between cities, and the total distance traveled.
public static void main(String[] args) {
TSPSolver solver = new TSPSolver();
int[][] distances = {
{0, 10, 15, 20},
{10, 0, 35, 25},
{15, 35, 0, 30},
{20, 25, 30, 0},
};
solver.solveTSP(distances); // Solve the TSP instance
}
Next the variables are being setup, where n is the total number of cities to be toured:
IntVar[] tour = model.intVarArray("tour", n, 0, n - 1); // Tour representing the order of cities visited
IntVar[] distance = model.intVarArray("distance", n, 0, 1000000); // Auxiliary variables for distances
IntVar totalDistance = model.intVar("totalDistance", 0, 1000000); // Total distance traveled
Constraint Setup
To ensure the tour adheres to the constraints of the TSP, I defined constraints using Choco-solver. This includes specifying the distances between cities and enforcing that the tour forms a single circuit, visiting each city exactly once.
for (int i = 0; i < n; i++) {
Tuples tuples = new Tuples(true); // Create tuples to represent valid combinations of city and distance
for (int j = 0; j < n; j++) {
if (j != i) {
tuples.add(j, distances[i][j]); // Add valid combinations of city and distance to tuples
}
}
model.table(tour[i], distance[i], tuples).post(); // Apply table constraint for each city
}
// Ensure that the tour forms a single circuit, visiting each city exactly once
model.subCircuit(tour, 0, model.intVar(n)).post();
}
Solver Configuration
I configured the solver to search for the optimal solution using a FirstFail search strategy, prioritizing smaller values during the search process.
Solver solver = model.getSolver();
solver.setSearch(
Search.intVarSearch(
new FirstFail(model), // Use FirstFail search strategy to select variables
new IntDomainMin(), // Priorities smaller values from domain of integer variables during search
distance));
Model Solving
Upon solving the model, I iterated through the solution to extract the optimal tour and total distance traveled. This information was then logged for analysis.
Map<Number, Integer[]> optimalSolution = new HashMap<>();
while (solver.solve()) {
Integer[] optimalTour = new Integer[n+1];
int current = 0; // Start from the first city
log.info("City {}", current); // Print the current city
optimalTour[0] = current;
for (int i = 1; i <= n; i++) {
int next = tour[current].getValue(); // Get the next city in the tour
optimalTour[i] = next;
log.info("City {}", next); // Print the next city
current = tour[current].getValue(); // Move to the next city
}
optimalSolution.put(totalDistance.getValue(), optimalTour);
log.info("\nTotal tour distance: {}", totalDistance.getValue()); // Print the total distance
}
Final TSPSolver
This is my final TSPSolver.java:
package example.micronaut;
import jakarta.inject.Singleton;
import lombok.extern.slf4j.Slf4j;
import org.chocosolver.solver.Model;
import org.chocosolver.solver.Solver;
import org.chocosolver.solver.constraints.extension.Tuples;
import org.chocosolver.solver.search.strategy.Search;
import org.chocosolver.solver.search.strategy.selectors.values.IntDomainMin;
import org.chocosolver.solver.search.strategy.selectors.variables.FirstFail;
import org.chocosolver.solver.variables.IntVar;
import java.util.HashMap;
import java.util.Map;
@Slf4j
@Singleton
public class TSPSolver {
public TSPSolution solveTSP(int[][] distances) {
int n = distances.length;
Model model = new Model("TSP");
// Variables
IntVar[] tour = model.intVarArray("tour", n, 0, n - 1); // Tour representing the order of cities visited
IntVar[] distance = model.intVarArray("distance", n, 0, 1000000); // Auxiliary variables for distances
IntVar totalDistance = model.intVar("totalDistance", 0, 1000000); // Total distance traveled
// Constraints
// Define the distances between cities using table constraints
for (int i = 0; i < n; i++) {
Tuples tuples = new Tuples(true); // Create tuples to represent valid combinations of city and distance
for (int j = 0; j < n; j++) {
if (j != i) {
tuples.add(j, distances[i][j]); // Add valid combinations of city and distance to tuples
}
}
model.table(tour[i], distance[i], tuples).post(); // Apply table constraint for each city
}
// Ensure that the tour forms a single circuit, visiting each city exactly once
model.subCircuit(tour, 0, model.intVar(n)).post();
// Define the objective: minimize the total distance traveled
model.sum(distance, "=", totalDistance).post();
model.setObjective(Model.MINIMIZE, totalDistance); // Set the objective to minimize total distance
// Solver setup
Solver solver = model.getSolver();
solver.setSearch(
Search.intVarSearch(
new FirstFail(model), // Use FirstFail search strategy to select variables
new IntDomainMin(), // Priorities smaller values from domain of integer variables during search
distance));
// Solve the Model and Display the Path
Map<Number, Integer[]> optimalSolution = new HashMap<>();
while (solver.solve()) {
Integer[] optimalTour = new Integer[n+1];
int current = 0; // Start from the first city
log.info("City {}", current); // Print the current city
optimalTour[0] = current;
for (int i = 1; i <= n; i++) {
int next = tour[current].getValue(); // Get the next city in the tour
optimalTour[i] = next;
log.info("City {}", next); // Print the next city
current = tour[current].getValue(); // Move to the next city
}
optimalSolution.put(totalDistance.getValue(), optimalTour);
log.info("Total tour distance: {}", totalDistance.getValue()); // Print the total distance
}
if (model.getSolver().hasObjective()) {
Number optimalDistance = model.getSolver().getBestSolutionValue(); // Get the optimal distance
log.info("Optimal tour distance: {}", optimalDistance);
return new TSPSolution(optimalSolution.get(optimalDistance), optimalDistance);
} else {
return null;
}
}
public static void main(String[] args) {
TSPSolver solver = new TSPSolver();
int[][] distances = {
{0, 10, 15, 20},
{10, 0, 35, 25},
{15, 35, 0, 30},
{20, 25, 30, 0},
};
solver.solveTSP(distances); // Solve the TSP instance
}
}
TSPSolution Model
To encapsulate the solution, I created a TSPSolution model using Lombok annotations, facilitating easy serialization and deserialization.
package example.micronaut;
import io.micronaut.serde.annotation.Serdeable;
import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;
@Data
@AllArgsConstructor
@NoArgsConstructor
@Serdeable.Serializable
public class TSPSolution {
private Integer[] optimalTour;
private Number totalDistance;
}
First attempt
For this simple case, the result is just as per expected:
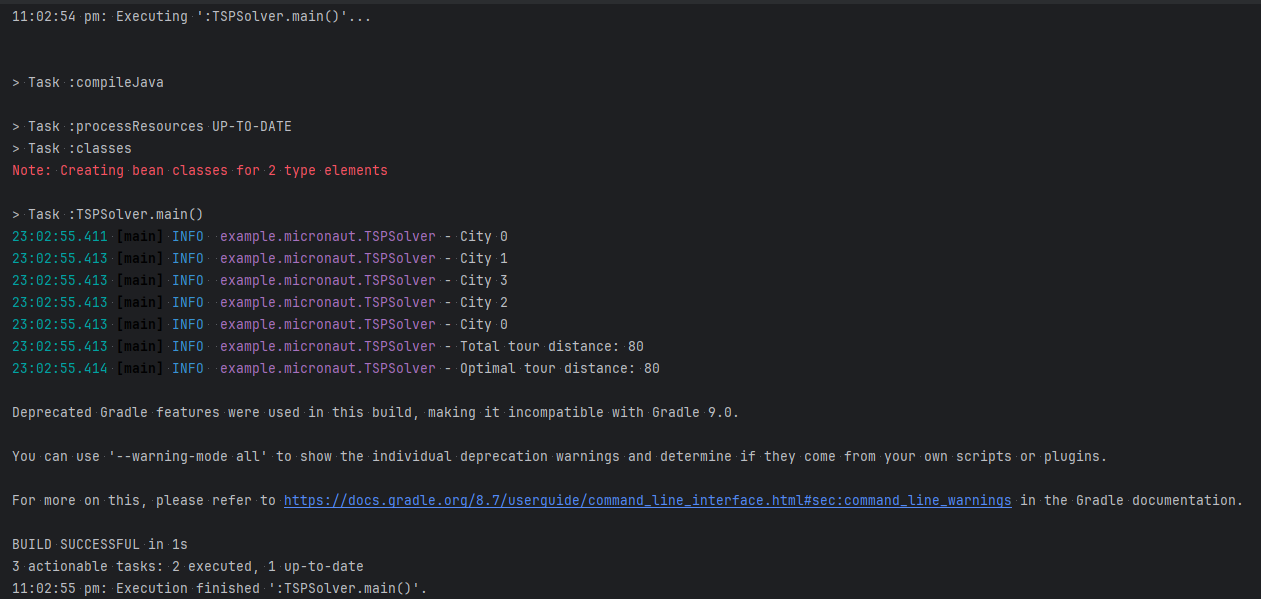
Converting to an API
To make the solution accessible as an API, I wrapped it within a controller class, TSPController.java, utilizing Micronaut annotations to define endpoints.
package example.micronaut;
import io.micronaut.http.MediaType;
import io.micronaut.http.annotation.*;
@Controller("/tsp")
public class TSPController {
private final TSPSolver tspSolver;
public TSPController(TSPSolver tspSolver) {
this.tspSolver = tspSolver;
}
@Post("/solve")
@Produces(MediaType.APPLICATION_JSON)
@Consumes(MediaType.APPLICATION_JSON)
public TSPSolution solveTSP(@Body int[][] distances) {
return tspSolver.solveTSP(distances);
}
}
Putting it in action
With the API set up, I tested various inputs using tools like Postman, observing the solutions returned for different scenarios.
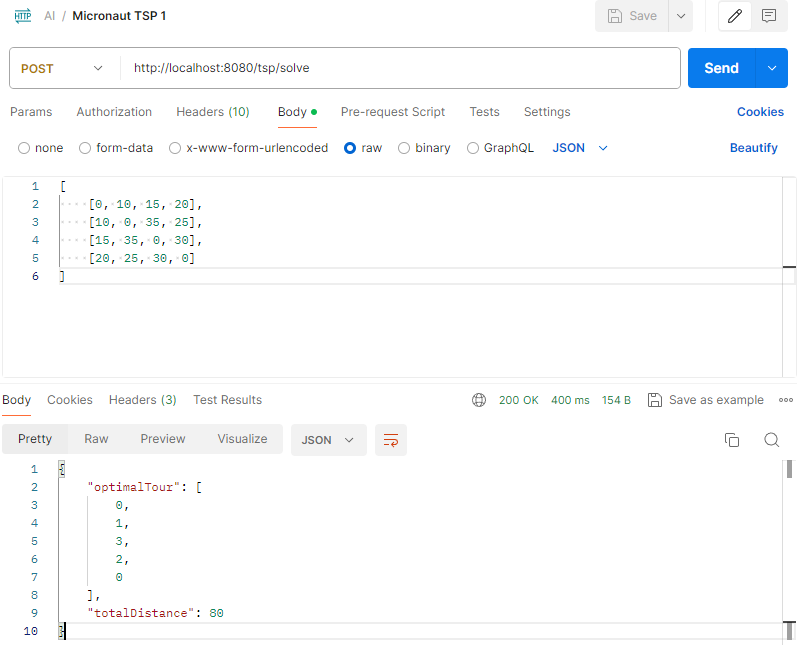
With the next set of inputs:
[
[0, 10, 15, 20, 25],
[10, 0, 35, 25, 20],
[15, 35, 0, 30, 10],
[20, 25, 30, 0, 15],
[25, 20, 10, 15, 0]
]
This is the result:
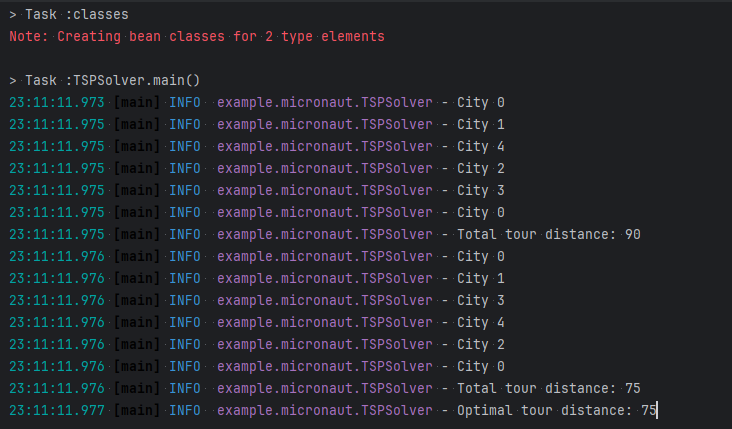
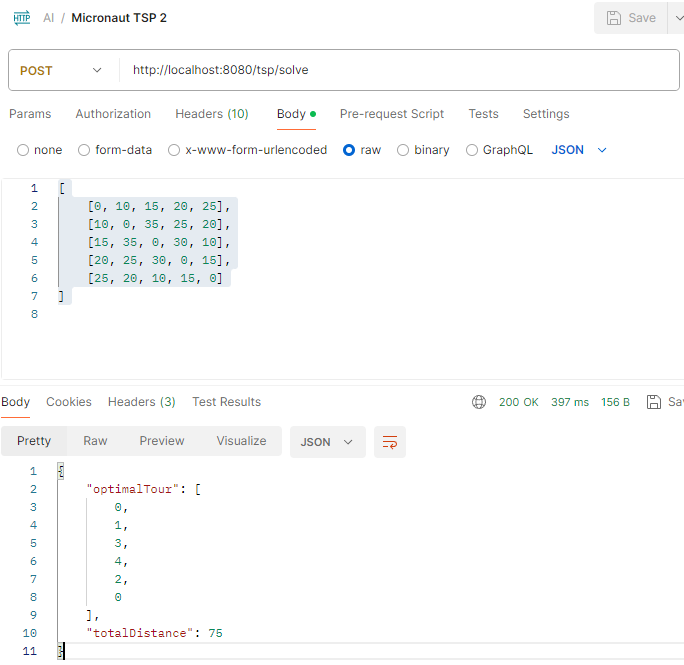
The final set of inputs:
[
[0, 10, 15, 20, 25, 30, 35, 40],
[10, 0, 35, 25, 20, 45, 50, 55],
[15, 35, 0, 30, 10, 40, 45, 60],
[20, 25, 30, 0, 15, 50, 55, 70],
[25, 20, 10, 15, 0, 35, 40, 65],
[30, 45, 40, 50, 35, 0, 25, 70],
[35, 50, 45, 55, 40, 25, 0, 75],
[40, 55, 60, 70, 65, 70, 75, 0]
]
The corresponding result:
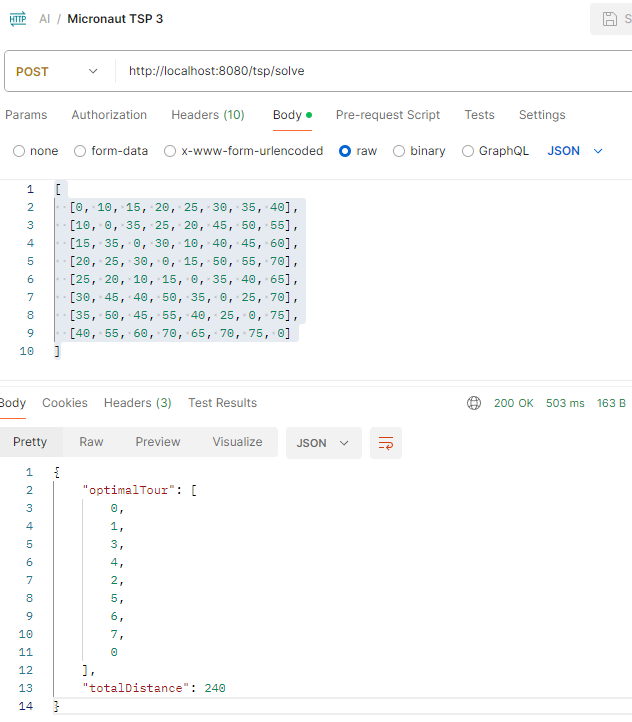
In conclusion, this project showcases the seamless integration of Choco-solver and Micronaut to solve the Travelling Salesman Problem efficiently and transform it into a versatile API. By harnessing the power of constraint programming and modern Java frameworks, we’ve demonstrated a robust solution for optimizing city tours. Whether you’re exploring algorithmic challenges or building real-world applications, this approach offers scalability, modularity, and performance. With further refinement and customization, this solution can be tailored to address a wide range of optimization problems in various domains.